Friends, when I have not been able to do my work properly due to mind control agents' altering my programs for past few days. Mind control agent tells me that several people keep on talking several things about me like that I have decided to not share my research with anyone. And many similar things that I do not like to share everything with people and other stuff like that.
I want to tell friends that I have been posting my good programs since 2016 on this thread. Many times I talk about some program and do not post it and that might be because that program might not be significant or might have a flaw so I do not share it. I have absolutely no qualms about sharing my programs and I want to request even those people who do not like me to take my programs and use them in their research in some helpful way and I would absolutely like if they find my programs helpful.
Anything like that I do not want to share my programs anymore is just not true. I want to continue my mathematics research all through my life and would like to continue to share many more interesting things with friends.
Now I want to come to their altering my programs. In fact, they had started to do it several days or more than a week before I started complaining about it. For example when I tried to find a nearest gamma density to 1D moments, I had enough success in my work but when I would check my results the next day, there would be just lukewarm success in my programs. This continued for a week and I was getting very worried that my research is not working properly and I still never thought that they were altering my programs. It was only when I realized that several programs went extremely well and I was very excited but the next day they would not work at all. Mind control agents had made this working model that I would do my research properly for a day until there was enough success but the next day they would alter it and I would be bogged down. I did not know for several days but some programs worked so well that they left strong impression on me and when they did not work the next day, I would become very worried that something was wrong. And then I realized this pattern of their altering my programs overnight.
Now mind control agent had been suggesting that I restart my research since they wanted to convince people that I am making up all of this thing about altering the programs since I no longer want to share my research with friends. I resisted and asked them to not alter the older programs and let me run them properly but they would not agree to it.
I want to tell friends that I absolutely love sharing my programs with friends because when all doors were closed on me, I was still able to find an expression for myself in a good way with my research and sharing it with friends. I would like to have some meanings and purpose of myself in a good way that contributes to society.
But living without my work and without programming and I have started to have pangs of depression over past few days when I stopped my programming work and it is very difficult therefore I have decided to restart my work and hope that they do not alter my new functions. This is despite that they have not allowed me to run many old functions properly.
Re: Breakthrough in the theory of stochastic differential equations and their simulation
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I was able to get my programs to work. I think many friends would already have run the good programs but, in case you have not, I am quickly posting the new versions of the main functions.
.
.
.
.
.
.
.
.
.
.
.
Here are the last few values when you run the main function.
YCoeffHH =
Columns 1 through 3
0 0 0.000000000000000
0.516150291626474 0.210155659504569 -0.002249247186387
0.079886307131609 0.038320722781206 -0.002914685934181
0.014238229495272 -0.005353846231259 -0.000206320558813
0.000582731628418 -0.000309388774534 -0.000049159883874
0.000885327028014 -0.000182860240725 -0.000045718758627
Columns 4 through 6
0 -0.000000000000000 -0.000000000000000
-0.000155390728398 -0.000514122151043 -0.000113510464299
-0.000102119083533 0.000024786488846 0.000012477074948
-0.000141263999664 -0.000037284412828 0.000003177506830
-0.000036100289804 -0.000005880156932 -0.000000606560238
-0.000009122837943 0.000000032256551 0.000000316430970
Look at output oof 2D Hermite-Series
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
YMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016162396242489 0.036215193260982
Columns 4 through 6
0.104307158908803 0.367014216578896 1.523776700116779
Look at comparison of second moments/moments
IndexMax =
201
YMomentsModel =
1.0e+02 *
Columns 1 through 3
0.017409823993282 0.036940044638198 0.092703856184305
Columns 4 through 6
0.269533422669167 0.895462482565601 3.370955049163986
DataMoments =
1.0e+02 *
Columns 1 through 3
0.017500827783291 0.037006085169492 0.091488739766061
Columns 4 through 6
0.258136573740686 0.815135310459562 2.833876685202050
Look at comparison of moments
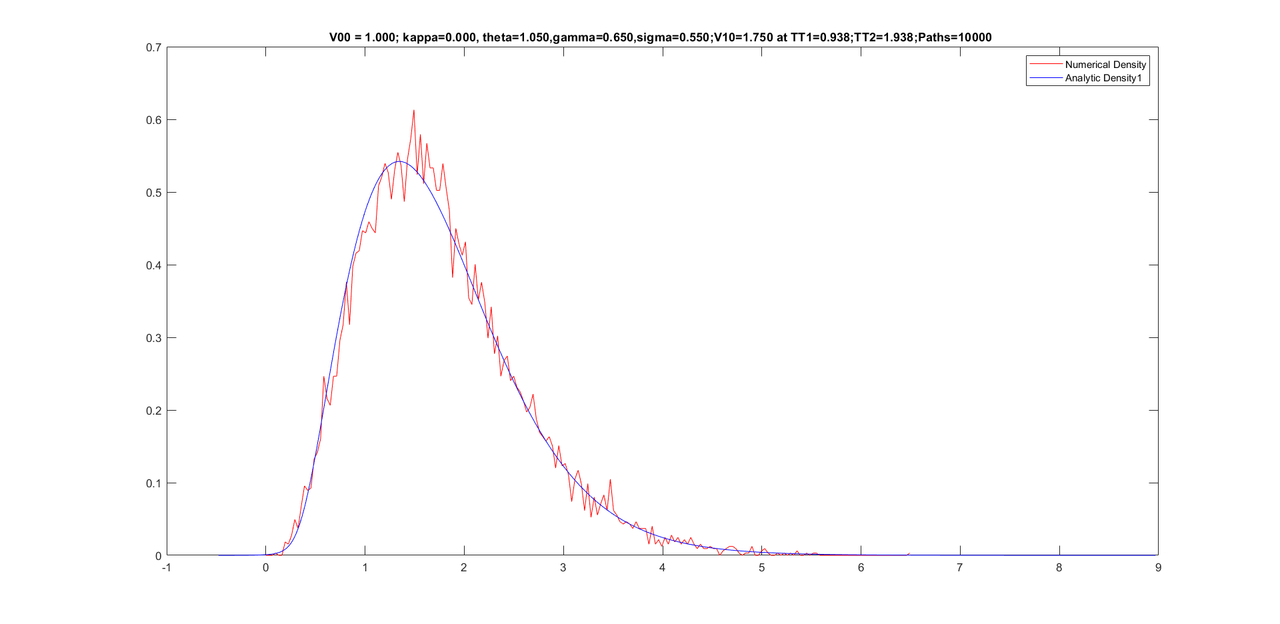
Look at density
This is the first version without altering the moments of conditional density
Here is the graph you see when you run the function.
.
.
.
.
.
.
Code: Select all
function []= ConditionalDensityHermitesBivariateNewtonItersRegSqr02()
%SV SDE is
%dV(t)=mu1 V(t)^beta1 dt+ mu2 V(t)^beta2 dt + sigma0 V(t)^gamma dZ(t)
%In mean reverting SDEs we ususally have
%mu1= kappaV * thetaV
%beta1=0
%mu2=-kappa
%beta2=0
Order=5;
%NDim=4;%Three assets and one SV.
NMomentsY=Order+1;
NMomentsX=Order+1;
w2D0(1:NMomentsY,1:NMomentsX)=1;
w2D5(1:NMomentsY,1:NMomentsX)=1;
w2D6(1:NMomentsY,1:NMomentsX)=1;
for nn=NMomentsY-1:-1:1
for mm=NMomentsX-1:-1:1
w2D5(nn,mm)=w2D5(nn+1,mm+1)*(nn+1).^5*(mm+1).^5.0;
w2D6(nn,mm)=w2D6(nn+1,mm+1)*(nn+1).^6*(mm+1).^6.0;
end
end
w2D0(1:NMomentsY,1:NMomentsX)=1;
w2Dh(1:NMomentsY,1:NMomentsX)=1;
w2D1(1:NMomentsY,1:NMomentsX)=1;
w2D2(1:NMomentsY,1:NMomentsX)=1;
w2D3(1:NMomentsY,1:NMomentsX)=1;
w2D4(1:NMomentsY,1:NMomentsX)=1;
for nn=NMomentsY-1:-1:1
for mm=NMomentsX-1:-1:1
w2Dh(nn,mm)=w2Dh(nn+1,mm+1)*(nn+1).^.5*(mm+1).^.5;
w2D1(nn,mm)=w2D1(nn+1,mm+1)*(nn+1)*(mm+1);
w2D2(nn,mm)=w2D2(nn+1,mm+1)*(nn+1).^2*(mm+1).^2.0;
w2D3(nn,mm)=w2D3(nn+1,mm+1)*(nn+1).^3*(mm+1).^3.0;
w2D4(nn,mm)=w2D4(nn+1,mm+1)*(nn+1).^4*(mm+1).^4.0;
end
end
%%%%%%%%%%%%%%%%%%%5
%%%%%%%%%%%%%%%%%%%5
V0=1.00;%.32;
V00=V0;
thetaV=1.050;%.045;%1;%.04;
kappaV=.000;%1.5;%1.5;
mu1=kappaV*thetaV;
mu2=-kappaV;
beta1=0;
beta2=1;
%gamma=.5;%.950;
%sigma0=.55;%.45;%
gamma=.65;%.950;.55
sigma0=.55;%.45;%.65
dt=.03125/2;
Tt=64*2;
T=Tt*dt;
seed0=52130649;
seed0=94210876;
rng(seed0, 'twister')
paths=10000;
V(1:paths,1)=V0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
TT1=60; %Transition distribution start
TT2=124; %Transition distribution end
Random2(1:paths/2,1)=0;
for tt=1:Tt
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
if(tt==TT1)
Xin(1:paths,1)=V(1:paths,1);
end
if(tt==TT2)
Yin(1:paths,1)=V(1:paths,1);
end
end
str=input("I have reached stone 1");
Order=5;
%
Ndata=paths;
%
[ZI] = MomentMatchedStandardNormalDiscretizedDensity(Ndata);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%55
[XCoeffH,Zx] = CalculateHermiteSeriesFromData01(Xin,Order,ZI);
[XCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(XCoeffH(1:Order+1),Order);
for qq1=1:Order+1
XMoments(qq1)=sum(Xin(1:paths).^qq1)/paths;
end
[XCoeffZ(1),XCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(XMoments,XCoeffZ(2:6));
[XCoeffH] = ConvertZSeriesToHermiteSeriesNew(XCoeffZ,Order);
for nn=1:paths
[Zx(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Xin(nn),XCoeffZ(1),XCoeffZ(2:6));
end
Zx0(1:Ndata,1)=Zx(1:Ndata);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[YCoeffH,Zy] = CalculateHermiteSeriesFromData01(Yin,Order,ZI);
[YCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffH(1:Order+1),Order);
for pp1=1:Order+1
YMoments(pp1)=sum(Yin(1:paths).^pp1)/paths;
end
[YCoeffZ(1),YCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YMoments,YCoeffZ(2:6));
%[YCoeffZ(1),YCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMoments02(YMoments);
[YCoeffH0] = ConvertZSeriesToHermiteSeriesNew(YCoeffZ,Order);
for nn=1:paths
[Zy(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Yin(nn),YCoeffZ(1),YCoeffZ(2:6));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
HH=5;
[CorrH] = CalculateCorrelationBivariateHermiteCH0(Zx,Zy,paths,HH)
CorrH
str=input("Look at hermites correlation");
Coeffyx2(1)=YCoeffH0(1);
Coeffyx2(2:6)=CorrH(1:5).*YCoeffH0(2:6);
Ydecorr(1:Ndata,1)=Yin(1:Ndata,1)-Coeffyx2(1) ...
-Coeffyx2(2).*Zx0(1:Ndata,1) ...
-Coeffyx2(3).*(Zx0(1:Ndata,1).^2-1) ...
-Coeffyx2(4).*(Zx0(1:Ndata,1).^3-3*Zx0(1:Ndata,1)) ...
-Coeffyx2(5).*(Zx0(1:Ndata,1).^4-6*Zx0(1:Ndata,1).^2+3) ...
-Coeffyx2(6).*(Zx0(1:Ndata,1).^5-10*Zx0(1:Ndata,1).^3+15*Zx0(1:Ndata,1));% ...
%-Coeffyx2(7).*(Zx0(1:Ndata,1).^6-15*Zx0(1:Ndata,1).^4+45*Zx0(1:Ndata,1).^2-15) ...
%-Coeffyx2(8).*(Zx0(1:Ndata,1).^7-21*Zx0(1:Ndata,1).^5+105*Zx0(1:Ndata,1).^3-105*Zx0(1:Ndata,1));% ...
clf;
Coeffyx2
PlotHermiteSeriesDensityAndRvGraph(Coeffyx2(1),Coeffyx2(2:Order+1),'b')
str=input("Look at initial correlated hermite series plot---2");
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[YdCoeffH,Zyd] = CalculateHermiteSeriesFromData01(Ydecorr,Order,ZI);
[YdCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YdCoeffH(1:Order+1),Order);
for pp1=1:Order+1
YdecorrMoments(pp1,1)=sum(Ydecorr(1:paths).^pp1)/paths;
end
[YdCoeffZ(1),YdCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YdecorrMoments,YdCoeffZ(2:6));
%[YdCoeffZ(1),YdCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMoments02(YdecorrMoments);
[YdCoeffH] = ConvertZSeriesToHermiteSeriesNew(YdCoeffZ,Order);
clf;
PlotHermiteSeriesDensityAndRvGraph(YdCoeffH(1),YdCoeffH(2:Order+1),'b')
str=input("Look at YdCoeffH density");
for nn=1:paths
[Zyd(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Ydecorr(nn),YdCoeffZ(1),YdCoeffZ(2:6));
end
Zyd0(1:paths,1)=Zyd(1:paths);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
YCoeffHH(1:6,1:6)=0.0;
YCoeffHH(2:6,1)=YdCoeffH(1,2:6);%*XCoeffRatio(1);
YCoeffHH
str=input("Look at 2D Hermite-series---5");
%%%%%%%%%%%%%%%%%%%%%%%%%%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YCoeffZ,MaxIter,w2D)
for pp1=1:Order+1
for qq1=1:Order+1
MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Ydecorr(1:paths,1).^pp1.*Xin(1:paths,1).^qq1)/paths;
%MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Ydecorr(1:paths,1).^pp1.*Zx0(1:paths,1).^qq1)/paths;
%MomentsYX(pp1,qq1)=sum((1:paths,1).^pp1.*Zx0(1:paths,1).^qq1)/paths;
end
end
% MomentsYX
% str=input("Look at cross-moments matrix");
MaxIter=150;
%In the function below, we do iterative optimization on all 2D Hermite
%coefficients excluding the first row. This function is applied when we
%have become too close to the true values by optimization through previous
%function.
%ZCoeffZ(1:6)=0;
%ZCoeffZ(2)=1;
%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D2);
%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd04(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D2);
%YCoeffHH
TargetCrossMoments=MomentsYX0;
OrderY=Order;
OrderX=Order;
%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd04(YCoeffHH,XCoeffZ,TargetCrossMoments,YdCoeffH,OrderY,OrderX,MaxIter);
MaxIter=1000;
[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D2);
% YObs(1:paths,1)=Ydecorr(1:paths,1);
% XObs(1:paths,1)=Xin(1:paths);
% %Zx0(1:paths,1)
% %Zyd(1:paths,1)
% XCoeffH0(1:Order+1,1)=XCoeffH(1:Order+1);
% %YdCoeffH(1:Order+1)
%
% [YCoeffHH,ObjFunc] = HSeriesCoeffsFromDataIterative2DDataA(YObs,XObs,YCoeffHH,XCoeffH0,Zx0,Zyd,YdCoeffH,MaxIter,Order,Ndata);
% %[ObjFuncBest] = Calculate2DObjWithData(YObs,XObs,YCoeffHH,XCoeffH,Hx,Hy,Ndata,Order);
%load("C:\Users\Lenovo\Documents\MATLAB\MATLAB1\pqfile02A.mat","YCoeffHH")%45000
YCoeffHH
str=input("Variable has been saved")
%YCoeffHH(6,:)=YCoeffHH(6,:);
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
%load("C:\Users\Lenovo\Documents\MATLAB\MATLAB1\pqfile02.mat","YCoeffZZ")%45000
MaxIter=2500;
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeriesSubset(YCoeffZZ,XCoeffZ,Order,MomentsYX0,YdecorrMoments,YdCoeffH,MaxIter);
%[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
%LG[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeries(YCoeffZZ,XCoeffZ,Order,MomentsYX0,YdecorrMoments,MaxIter);
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeriesWithData(YCoeffZZ,XCoeffZ,Order,MomentsYX0,YdecorrMoments,MaxIter);%,Zyd,Zx,Ndata);
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeriesWithData(YCoeffZZ,ZCoeff,Order,MomentsYX0,MomentsY,MaxIter,Zyd,Zx,Ndata);
%[YdecorrMomentsM] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);
%YdecorrMomentsM
%YdecorrMoments
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[YdecorrMomentsM] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);
YdecorrMomentsM
YdecorrMoments
str=input("Look at comparison of moments")
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[YCoeffHH] = ConvertZSeriesToHermiteSeries2D(YCoeffZZ,Order+1,Order+1);
YCoeffHH
str=input("Look at output oof 2D Hermite-Series");
YCoeffHH(1,1:Order+1)=YCoeffHH(1,1:Order+1)*0+Coeffyx2(1,1:Order+1);
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
[Y1DMoments]=CalculateMomentsOfZSeries(YCoeffZ(1),YCoeffZ(2:6),5,6)
OrderY=Order;
OrderX=Order;
NMoments=6;
[YMoments] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,OrderY,OrderX,NMoments);
%
%
Y1DMoments
YMoments
str=input("Look at comparison of second moments/moments");
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%In this block, we do conditional Monte Carlo of SDE which is the true
%numerical 1D conditional density of Y conditional on X having a given
%value. This value of X on which we are conditionin is defined by V10 below.
%We can alter V10 below and it will take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
%Zx=2.0;
%V10=XCoeffZ(1)+XCoeffZ(2).*Zx+XCoeffZ(3).*Zx^2+XCoeffZ(4).*Zx^3+XCoeffZ(5).*Zx^4+XCoeffZ(6).*Zx^5;
%V10
%str=input("Look at V10");
V10=1.750;
V(1:paths)=V10;
Random2(1:paths,1)=0;
for tt=TT1+1:TT2
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
end
%Below
NoOfBins=200;
MaxCutOff=10;
[XDensity,IndexOut,IndexMax] = MakeDensityFromSimulation_Infiniti_NEW(V,paths,NoOfBins,MaxCutOff );
clf;
plot(IndexOut(1:IndexMax),XDensity(1:IndexMax),'r');
hold on
for qq=1:6
DataMoments(qq)=sum(V(:).^qq)/paths;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%Below, we calculate the value of Zx0 corresponding to X0 (here V10). This
%comes from inverting the Z-series of X so that X=V10;
xOrder=Order;
yOrder=Order;
[Zx0] = CalculateZgivenXAndHSeriesCoeffs(V10,XCoeffH,xOrder);
%Below, we collapse two dimensional pdf of Y|X to one dimensional pdf given
%Zx i.e. this Y|X=X(Zx)
%Here we take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
He(1)=1;
He(2)=Zx0;
He(3)=Zx0^2-1;
He(4)=Zx0^3-3*Zx0;
He(5)=Zx0^4-6*Zx0.^2+3;
He(6)=Zx0^5-10*Zx0.^3+15*Zx0;
He(7)=Zx0^6-15*Zx0.^4+45*Zx0.^2-15;
He(8)=Zx0^7-21*Zx0.^5+105*Zx0.^3-105*Zx0;
YCoeffh(1:Order+1)=0;
for hh=1:yOrder+1
for hh2=1:xOrder+1
YCoeffh(hh)=YCoeffh(hh)+YCoeffHH(hh,hh2).*He(hh2);
end
end
[YCoeffz(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffh(1:Order+1),Order);
[YMomentsModel]=CalculateMomentsOfZSeries(YCoeffz(1),YCoeffz(2:6),5,6);
YMomentsModel
DataMoments
str=input("Look at comparison of moments");
PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh(2:yOrder+1),'b')
%hold on
%PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh1(2:yOrder+1),'g')
title(sprintf('V00 = %.3f; kappa=%.3f, theta=%.3f,gamma=%.3f,sigma=%.3f;V10=%.3f at TT1=%.3f;TT2=%.3f;Paths=%d ',V00, kappaV, thetaV,gamma,sigma0, V10,(TT1*dt),(TT2*dt),paths));%,sprintf('theta= %f', theta), sprintf('kappa = %f', kappa),sprintf('sigma = %f', sigma0),sprintf('T = %f', T));
legend({'Numerical Density','Analytic Density1'}, ...
'Location','northeast')
str=input("This is the first version without altering the moments of conditional density")
[YMoments0]=CalculateMomentsOfZSeries(YCoeffz(1),YCoeffz(2:6),5,6)
end.
.
.
Code: Select all
function [YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D)
SeriesOrder=6;
NMoments=6;
Order=5;
VarY(2:Order+1)=0.0;
for nn=2:Order+1
SD(nn)=sqrt(YCoeffHH(nn,1).^2+YCoeffHH(nn,2).^2+YCoeffHH(nn,2).^2*2+YCoeffHH(nn,4).^2*6+YCoeffHH(nn,5).^2*24+YCoeffHH(nn,6).^2*120);
if(SD(nn)>YdCoeffH(nn)*1.005)
YCoeffHH(nn,1:Order+1)=YCoeffHH(nn,1:Order+1).*(YdCoeffH(nn)./SD(nn))*1.005;
end
end
%[YdMoments]=CalculateMomentsOfZSeries(YdCoeffZ(1),YdCoeffZ(2:6),5,6);
% %Below, we calculate first and 2nd moment of 2D Hermite series
% [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHH,Order,Order);
% %VarHH is model variance .
% VarHH=M2HH-MeanHH.^2;
% %VarIn is input variance
% VarIn=YMoments(2)-YMoments(1).^2;
% %Variance correction is applied below to all rows but not to first row of hermite series.
% %YCoeffHH(2:6,1:6)=YCoeffHH(2:6,1:6).*sqrt(VarIn/VarHH);
% %YCoeffHH(1,2:6)=YCoeffHH(1,2:6).*sqrt(VarIn/VarHH);
% %We convert final 2D Hermite series to 2D Z-series
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
for nn=1:SeriesOrder
for mm=1:SeriesOrder
DeltaX(nn,mm)=.00125*2/(factorial(nn+1))/(factorial(mm+1));%/2^((nn-1)/2)/2^((mm-1)/2);
DeltaXMax(nn,mm)=DeltaX(nn,mm)*10;
end
end
ObjFunc1=0;
ObjFunc2=0;
%%%Weights on objective function that shows fit to moments
w2D(NMoments,NMoments)=1;
for nn=NMoments-1:-1:1
for mm=NMoments-1:-1:1
w2D(nn,mm)=w2D(nn+1,mm+1)*(nn+1).^0*(mm+1).^0;
end
end
[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZ,XCoeffZ,Order,Order);
[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);
for pp1=1:Order+1
for qq1=1:Order+1
Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
end
% Moments1D(pp1)=AMat((Order+1)*(Order+1)+pp1,1);
end
[ObjFuncBest] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
%ObjFuncBest=ObjFuncBest+sum((BMat-YdMoments).^2);
%[ObjFuncBest] = CalculateObjMoment(sMu,Moments,w,mOrder);
ObjFuncBest
str=input("Look objFuncBest");
%cBest=c;
ImproveFlag(1:SeriesOrder,1:SeriesOrder)=1;
ImproveFlagPrev(1:SeriesOrder,1:SeriesOrder)=0;
ImproveCount(1:SeriesOrder,1:SeriesOrder)=0;
SeriesOrderM=6;
kk=0;
while ((kk<MaxIter)&&(ObjFuncBest>.001))
kk=kk+1;
%We only iteratively alter c(2:7), first and second moments are
%retrieved automatically in our set up
for nn=2:6%SeriesOrder
for mm=1:6%SeriesOrder
if((nn==1))
% ;
else
ImproveFlagPrev(nn,mm)=ImproveFlag(nn,mm);
YCoeffHHnew=YCoeffHH;
YCoeffHHnew(nn,mm)=YCoeffHHnew(nn,mm)+DeltaX(nn,mm);
YSD(nn)=sqrt(YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,3).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120);
if(YSD(nn)>abs(YdCoeffH(nn))*1.005)
YCoeffHHnew(nn,:)=YCoeffHHnew(nn,:).*abs(YdCoeffH(nn))./YSD(nn)*1.005;
end
%
% if(nn>1)
% VarY(nn)=YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,2).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120;
% if(VarY(nn)>1.15^2*YdCoeffH(nn).^2)
% YCoeffHHnew(nn,1:Order+1)=YCoeffHHnew(nn,1:Order+1).*sqrt(YdCoeffH(nn).^2./VarY(nn))*1.15;
% end
% end
%Below, we calculate first and 2nd moment of 2D Hermite series
% [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHHnew,Order,Order);
%VarHH is model variance .
% VarHH=M2HH-MeanHH.^2;
%VarIn is input variance
% VarIn=YMoments(2)-YMoments(1).^2;
%Variance correction is applied below to all rows but not to first row of hermite series.
% YCoeffHHnew(2:6,1:6)=YCoeffHHnew(2:6,1:6).*sqrt(VarIn/VarHH);
% YCoeffHHnew(1,2:6)=YCoeffHHnew(1,2:6).*sqrt(VarIn/VarHH);
%We convert final 2D Hermite series to 2D Z-series
[YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
for pp1=1:Order+1
for qq1=1:Order+1
Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
end
end
[ObjFunc1] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZnew,Order,Order,Order+1);
%ObjFunc1=ObjFunc1+sum((BMat-YdMoments).^2);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.0,Order);
DFlag1=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.0,Order);
DFlag2=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
%DValue1=1;
%DValue2=1;
%DFlag1=1;
%DFlag2=1;
if((ObjFunc1<ObjFuncBest)&&(DFlag1==1)&&(DFlag2==1))
%if(ObjFunc1<ObjFuncBest)
ObjFuncBest=ObjFunc1;
YCoeffHH=YCoeffHHnew;
ImproveFlag(nn,mm)=1;
else
YCoeffHHnew=YCoeffHH;
YCoeffHHnew(nn,mm)=YCoeffHHnew(nn,mm)-DeltaX(nn,mm);
%
% YSD(nn)=sqrt(YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,3).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120);
%
if(YSD(nn)>abs(YdCoeffH(nn))*1.005)
YCoeffHHnew(nn,:)=YCoeffHHnew(nn,:).*abs(YdCoeffH(nn))./YSD(nn)*1.005;
end
%
% if(nn>1)
% VarY(nn)=YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,2).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120;
% if(VarY(nn)>1.15^2*YdCoeffH(nn).^2)
% YCoeffHHnew(nn,1:Order+1)=YCoeffHHnew(nn,1:Order+1).*sqrt(YdCoeffH(nn).^2./VarY(nn))*1.15;
% end
% end
%Below, we calculate first and 2nd moment of 2D Hermite series
% [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHHnew,Order,Order);
%VarHH is model variance .
% VarHH=M2HH-MeanHH.^2;
%VarIn is input variance
% VarIn=YMoments(2)-YMoments(1).^2;
%Variance correction is applied below to all rows but not to first row of hermite series.
% YCoeffHHnew(2:6,1:6)=YCoeffHHnew(2:6,1:6).*sqrt(VarIn/VarHH);
% YCoeffHHnew(1,2:6)=YCoeffHHnew(1,2:6).*sqrt(VarIn/VarHH);
%We convert final 2D Hermite series to 2D Z-series
[YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
for pp1=1:Order+1
for qq1=1:Order+1
Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
end
end
[ObjFunc2] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZnew,Order,Order,Order+1);
% ObjFunc2=ObjFunc2+sum((BMat-YdMoments).^2);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.0,Order);
DFlag1=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.0,Order);
DFlag2=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
%DValue1=1;
%DValue2=1;
%DFlag1=1;
%DFlag2=1;
if((ObjFunc2<ObjFuncBest)&&(DFlag1==1)&&(DFlag2==1))
% if(ObjFunc2<ObjFuncBest)
ObjFuncBest=ObjFunc2;
YCoeffHH=YCoeffHHnew;
ImproveFlag(nn,mm)=-1;
else
ImproveFlag(nn,mm)=0;
end
end
end
end
end
if(rem(kk,1)==0)
kk
ObjFunc1
ObjFunc2
ObjFuncBest
YCoeffHH
ImproveCount
end
ImproveFlag0=0;
for nn=1:SeriesOrder
for mm=1:SeriesOrder
if(ImproveFlag(nn,mm)==0)
DeltaX(nn,mm)=DeltaX(nn,mm)*.88;
%ImproveFlag0=1;
end
if((ImproveFlag(nn,mm)==1)||(ImproveFlag(nn,mm)==-1))
DeltaX(nn,mm)=DeltaX(nn,mm)*1.1;
%ImproveFlag0=1;
end
if(DeltaX(nn,mm)>DeltaXMax(nn,mm))
DeltaX(nn,mm)=DeltaXMax(nn,mm);
end
end
end
end
ObjFunc=ObjFuncBest;
end.
.
Here are the last few values when you run the main function.
YCoeffHH =
Columns 1 through 3
0 0 0.000000000000000
0.516150291626474 0.210155659504569 -0.002249247186387
0.079886307131609 0.038320722781206 -0.002914685934181
0.014238229495272 -0.005353846231259 -0.000206320558813
0.000582731628418 -0.000309388774534 -0.000049159883874
0.000885327028014 -0.000182860240725 -0.000045718758627
Columns 4 through 6
0 -0.000000000000000 -0.000000000000000
-0.000155390728398 -0.000514122151043 -0.000113510464299
-0.000102119083533 0.000024786488846 0.000012477074948
-0.000141263999664 -0.000037284412828 0.000003177506830
-0.000036100289804 -0.000005880156932 -0.000000606560238
-0.000009122837943 0.000000032256551 0.000000316430970
Look at output oof 2D Hermite-Series
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
YMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016162396242489 0.036215193260982
Columns 4 through 6
0.104307158908803 0.367014216578896 1.523776700116779
Look at comparison of second moments/moments
IndexMax =
201
YMomentsModel =
1.0e+02 *
Columns 1 through 3
0.017409823993282 0.036940044638198 0.092703856184305
Columns 4 through 6
0.269533422669167 0.895462482565601 3.370955049163986
DataMoments =
1.0e+02 *
Columns 1 through 3
0.017500827783291 0.037006085169492 0.091488739766061
Columns 4 through 6
0.258136573740686 0.815135310459562 2.833876685202050
Look at comparison of moments
Look at density
This is the first version without altering the moments of conditional density
Here is the graph you see when you run the function.
.
.

You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, in next 2-3 days, I want to write a more general function that is also better from the programming practices perspective and also faster and can also calibrate a 8 X 8 2D Hermite series. I hope that everything goes well and I would love to post a better and more general version of the program. I wanted to do it 7-10 days ago but got bogged down by the other problems. I hope that things remain better now.
The volatility regime in the program of last post is about the maximum you can do with a 6X6 2D Hermite series and for more volatility, we would have to use a 8X8 2D Hermite series.
The volatility regime in the program of last post is about the maximum you can do with a 6X6 2D Hermite series and for more volatility, we would have to use a 8X8 2D Hermite series.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
