-
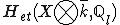
- rockinsquat
- Posts: 1
- Joined:
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
Hi all,My problem is the following : I have two liquid currencies pairs cc1/cc2 (rate [$]S_t^{1,2}[$]) and cc1/cc3 (rate [$]S_t^{1,3}[$]) whose implied volatilies are known, and I must calculate the implied volatility of the illiquid currency pair cc3/cc2 (rate [$]S_t^{32} = S_t^{1,2} / S_t^{1,3}[$]), and I must do it by using a gaussian copula.Let T be a given maturity, I calculate the densities of rates [$]S_T^{1,2}[$] and [$]S_T^{1,3}[$] (this is fully backtested and works very good) and from this and from a given rho, I want to calculate the implied vol [$]\sigma(T,K)[$] of cc3/cc2 for some given strike K.To do this, I can start by computing the price of a call on [$]S_T^{32}[$] of maturity T and strike K, and then finish by simply impliciting the vol (this step is fully backtested and works perfectly, I used Jaeckel's algorithm.) So my only problem remains the calculation of the price of a call on [$]S_T^{32}[$] of maturity T and strike K.I wrote it as a double integral where on each axis of integration strikes for both currencies rates are ranging around the corresponding forwards, the lower and upper bounds around the forward being given by the corresponding forward multiplied or divided by a correction of 8 standard deviation exp(vol*sqrt(T)*8) where vol is the implied vol of the corresponding forward. Over the [$]S_t^{1,3}[$]-integration axis I do a fine gauss-legendre integration, and then over the [$]S_t^{1,2}[$]-axis I use a simple trapezoid rule. Doing this for various strikes and maturities gives an implied vol surface S1 to me, that is quite ok.But, I have a problem. If, in all the previous stuff, I swap 1 and 2 and 1 and 3, that is, I start from cc2/cc1 and cc1/cc3, the cross implied vol that I will get at the end will be the one for the cross currency cc2/cc3. To get the one for cc3/cc2, I simply use two facts : 1) calls and puts have the same implied volatility and 2) the implied vol of call (T,K) on cc3/cc2 is by non arbitrage equal to the implied vol of put on cc2/cc3 of maturity T and strike 1/K. This gives to me a second implied vol surface S2 for cc3/cc2, but the problem is that the first one S1 smiles  whereas the second S2 is more in a sulk like :-\.I would say that my 2D cubature rule (gauss-legendre one the first dimension then trapezoidal on the second) somehow breaks the K <--> 1/K symmetry, causing the smile defect of the second surface S2, but I'm not sure.Do you have any idea ? What 2D integration rule would you use, if the issue is there ?Thx a lot !PS : I posted first in the technical forum, but I think here it is more well-suited. Didn't manage to find a way of suppressing the initial post.
whereas the second S2 is more in a sulk like :-\.I would say that my 2D cubature rule (gauss-legendre one the first dimension then trapezoidal on the second) somehow breaks the K <--> 1/K symmetry, causing the smile defect of the second surface S2, but I'm not sure.Do you have any idea ? What 2D integration rule would you use, if the issue is there ?Thx a lot !PS : I posted first in the technical forum, but I think here it is more well-suited. Didn't manage to find a way of suppressing the initial post.
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
I would check that each step of your procedure preserves the desired foreign-domestic symmetry, starting with the liquid pairs alone
-
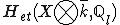
- rockinsquat
- Posts: 1
- Joined:
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
Hi Alan, yes, I forgot to say that yes, everything except the integration part is invariant indeed for the desired for/dom symmetry. That's why I spotted the integration part finally. Now, I refined the grids, and it's ok, but a bit too slow - logical.What are the best 2D cubature formulas that are not "product" of 1D integration rules ?
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
I don't know -- I just use NIntegrate in Mathematica
-

- Cuchulainn
- Posts: 23029
- Joined:
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
QuoteOriginally posted by: rockinsquatHi Alan, yes, I forgot to say that yes, everything except the integration part is invariant indeed for the desired for/dom symmetry. That's why I spotted the integration part finally. Now, I refined the grids, and it's ok, but a bit too slow - logical.What are the best 2D cubature formulas that are not "product" of 1D integration rules ?Depends on how many dimensions.What about Monte Carlo?
Last edited by Cuchulainn on April 5th, 2014, 10:00 pm, edited 1 time in total.
-
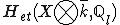
- rockinsquat
- Posts: 1
- Joined:
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
When I ask what are the best 2D cubature formulas that are not "product" of 1D integration rules, the dimension D is 2.I'm by the way interested in quadrature formulas, not in monte carlo.
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
QuoteOriginally posted by: rockinsquatDo you have any idea? What 2D integration rule would you use, if the issue is there ?Have you tried Padua points? Here some Matlab code, or do you prefer C++? Maybe not the optimal ones, but given for varous accuracies and the most common and practical rule.
-

- Cuchulainn
- Posts: 23029
- Joined:
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
Why not use GL20 on GL20? I hv written VBA that does that works fine for me - if u want sample u can pm me - I did post here my codes but I think it's better u pm me and I send u snippet.
Last edited by geneboo on June 1st, 2014, 10:00 pm, edited 1 time in total.
-
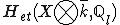
- rockinsquat
- Posts: 1
- Joined:
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
Actually, the problem was not the integration, but the bounds of integration. As it linked to implied densities, and finally not really a numerical problem (I tried trapezoidal 400 * trapezoidal 400, and also Riemann * Riemann) I will "migrate" my question in the technical forum, to give more details.
Copulas and implied vol of cc3/cc2 knowing implied vol surfaces of cc1/cc2 and cc1/cc3 : a 2D integration issue
Well, bounds are always tricky - but if you're going to do integration that is based on normal probability - i usually choose bounds of -10 till 10... if the tails are fat though...
