if the global derivatives conference is a good indicator, rough volatility seems to be one of the hottest things in quantitative pornography these days.

what is it exactly and why is it attractive (without going into technical details)?

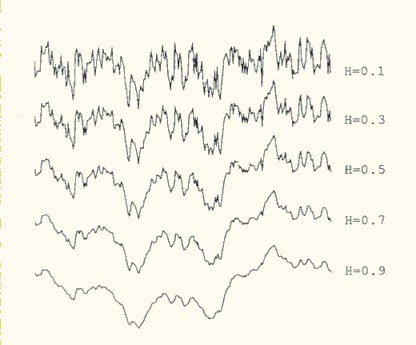
Never heard of it, but it looks like they suggest to model the spot vol process with fractional Brownian motion?  ..like H=0.1 in te plot below.

H=0.5 is classic Brownian motion H>0.5 is persistence / positive autocorrelation, H<0.5 is anti-persistence. H comes from "Hust". H<>0.5 mean that you have auto correlation across all time scales.

H is also how standard deviation scales across timesteps. With BM you have sqrt(t) = t^0.5 = t^H

What are your thoughts?

From what I've read (and not understood) is as you  said they try to model it as fBM. But it is not clear to me why model it as fBM. Is it to control the auto-correlation, and if so, are there no other ways to control / model auto-correlation using something else than fBM? 

Trying to grasp what the advantage would be of using fBM.

I had the exact same question. I think fBM has a single variable, H whereas having an autocorrelation vector will have lots of variables, and lots of stability/calibration precision issues?
If fBM gives a nice fit to observations, and if it leads to analytical solutions then it can be good simple improvement over existing models?
Personally I'm a bit skeptical towards fBM, I'm not a big fan of idealized models that model things across timescales that span orders of magnitude. However, it might be a very good model in the set of models that have very little variables.

It's supposed to give nice fit to observations, and even predict volatility accurately (very suspicious ), but afaik it's not that simple. E.g. integration of fBM, Ito's or Ito-like formula for fBM etc - I dont know if these things are well-defined / uniquely defined.

I have to say though, Outrun, looking at your figures for H=0.1 and H = 0.3, those do look realistic. Did you simulate those paths yourself, I think you already have quite some experience with simulation of fBM?

Oh no, I have little experience with fBM, but I've had a long time interest in chaotic systems, non linear dynamics, fractal dimension measures etc .

There is a class of distributions that keep their shape under addition, but which grow with a different rate than sqrt, the alpha stable distributions. Those are however not analytical from what I remember.

To simulate fBM I would start with discrete timesteos of your path, then compute the covariance matrix which is uniquely​ defined by H, then do a Cholesky and use that to correlate independent gaussians to the target covariance.?

I heard Jim Gatheral give a talk on this at Baruch College.I think it is a good place to start.

https://arxiv.org/abs/1410.3394

Simulations with fBM with Hurst exponent >0.8 respect the long-term memory feature in the process.  That is high autocorrelation for months at a time (simulated).  The whole autocorrelation profile changes from exponential decay  exp(t2 - t1) to power law  (t2 - t1)^(...).

This fits the behaviour of interest rates -- if we study time series of a forward rate about particular tenor over time.

I heard Jim Gatheral give a talk on this at Baruch College.I think it is a good place to start.

https://arxiv.org/abs/1410.3394

can you give us directions to Baruch College then?

I heard Jim Gatheral give a talk on this at Baruch College.I think it is a good place to start.

https://arxiv.org/abs/1410.3394

can you give us directions to Baruch College then?

Across the road from the "Fighting" 69th Armory.