I wish to emulate a random market on a locally implemented matching engine. There are many use cases of such environment including further training and competition of non-random bots, but it's a different topic.

Since price (and all data driven indicators) is a deterministic function of orders and the matching algorithm, it's reasonable to model random "traders" (i.e. or random orders) instead of random price. Here are a couple of directions that I consider:

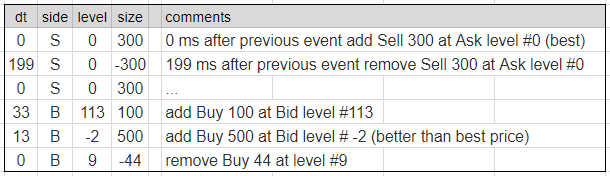
1. Based on historical order-by-order full depth data. Suppose, I convert millions of data events into a form like this:

• dT - time diff from the previous event
• ActionType - Send or Cancel or Modify an order
• Side - Buy or Sell
• PriceLevel - relative distance to the best Bid/Ask according the side Buy or Sell (aggressive orders can be represented by "negative distance")
• Quantity - size of the order

Then at each step my random bot randomly selects an action from this list and executes it.

2. Similar to the above, but each of these fields will have a separate probability distribution. These distributions can still be derived from empirical/historical data, but the resulting action in most cases will not be a replication of any of actions in the original data.

What model do you think is better? Both seem simple to implement, but the first model requires to solve the cases of cancel or modify actions when order of such size doesn't exist at specified price level. Alternatively, I can implement both, and let them compete with each other. Are there additional models of random orders / traders?

2 sounds like a typical newbie overkill.

So you end up with 5 probability distributions. Or 10. Each of them has presumably at least two parameters. Some maybe more.

What do you calibrate them to? What does the copula look like? Can you even distinguish between a "good" and "bad" point in the parameter space?

1 is more like it, but it hasn't been thought out properly. "at each step my random bot randomly selects an action from this list and executes it". Say it selects "dT". How does it "execute" "dT"?

Most orderbook models start with some jump model for order arrivals. The model has a jump arrival rate (dT) and a distribution of jump sizes which tells you that an order at touch is more likely than an order at touch minus 10,000 ticks. If you have to, add a similar process for cancellations.

That you can usually calibrate to some steady state shapes of the orderbook and some event rates.

The difference between passive and aggressive is for all intents and purposes non-existent at this level. Aggressive can be modelled as passive on the other side of the spread, modulo GFD vs IOC. Modify is also not a thing - most modify orders are actually cancel-replace orders.

There are many orderbook models. Start with Jim Gatheral's slides here, and look up the references.
I know it's ten years old. But you have to start somewhere.

Thanks for the answer, figaro. 
>> What do you calibrate them to?
The aim is pretty vague. I want to make this market behave "naturally", i.e. to make it difficult to distinguish it from real market. 

To clarify, I do not intend to model the price, but to model the actions, i.e. sending / canceling orders, which will be processed by locally made matching engine and thus produce the price and everything else, including the order book. This is in contrast to the order book modeling in the article that you shared. Also, I prefer to avoid fitting empirical distributions by known probability distributions. Instead, I can use empirical distributions as is. Here is an example:


Note that negative level means price improvement, which may or may not generate a trade.

>> Say it selects "dT". How does it "execute" "dT"?
Method #1 means that the bot randomly selects one of millions of such actions and executes it dT time after the previous action, and so on. Here dT is in milliseconds, but it can be microseconds as well. It will be needed to run multiple bots in parallel.

Method #2 means using empirical distributions of each column separately. But as you mentioned, the update rate depends on distance from the market. This can be addressed by using joint distribution of level and size. Buy/sell distribution can be simply 50%, and dt - as a separate distribution taken from the data.

Does this make sense? If yes, the only problem left is how to emulate "overnight" orders which provide initial order book. One approach is to use such orders from the data, but randomizing buy/sell side. Any better ideas would be appreciated.

Well, it is still the same underlying problem.

In all cases, your process is:
- select random time dT
- select random price level S
- select random quanitity Q
- select random action 0 (add liquidity) or 1 (subtract liquidity)
- in case of subtract liquidty, check that you are not subtracting more than there is
- execute action.
You can use a two-tailed distribution for S to model the entire book, or two separate one-tailed distributions to model each side separately. It's the same thing.

The process of selecting dT and S is a jump model. That is what jump models are. What you need is called a "finite intensity" jump model, i.e. you want a finite number of jumps in any finite interval. There are also inifinite intensity models, where you have continuous jumps.

You still have to specify the distributions that you are drawing dT, S and Q from. And that is the same thing as calibrating to a steady state orderbook shape, plus relaxation speed at which it approaches that steady state.

Drawing from some empirical distributions is theoretically the same thing, but practically there is a ton of complications. Most importantly, intraday seasonality coupled with finite data sets.

If you want to start with a half-full book, the simplest thing is to just start the simulation a bit before your open, without crossing.