Friends, when I have not been able to do my work properly due to mind control agents' altering my programs for past few days. Mind control agent tells me that several people keep on talking several things about me like that I have decided to not share my research with anyone. And many similar things that I do not like to share everything with people and other stuff like that.
I want to tell friends that I have been posting my good programs since 2016 on this thread. Many times I talk about some program and do not post it and that might be because that program might not be significant or might have a flaw so I do not share it. I have absolutely no qualms about sharing my programs and I want to request even those people who do not like me to take my programs and use them in their research in some helpful way and I would absolutely like if they find my programs helpful.
Anything like that I do not want to share my programs anymore is just not true. I want to continue my mathematics research all through my life and would like to continue to share many more interesting things with friends.
Now I want to come to their altering my programs. In fact, they had started to do it several days or more than a week before I started complaining about it. For example when I tried to find a nearest gamma density to 1D moments, I had enough success in my work but when I would check my results the next day, there would be just lukewarm success in my programs. This continued for a week and I was getting very worried that my research is not working properly and I still never thought that they were altering my programs. It was only when I realized that several programs went extremely well and I was very excited but the next day they would not work at all. Mind control agents had made this working model that I would do my research properly for a day until there was enough success but the next day they would alter it and I would be bogged down. I did not know for several days but some programs worked so well that they left strong impression on me and when they did not work the next day, I would become very worried that something was wrong. And then I realized this pattern of their altering my programs overnight.
Now mind control agent had been suggesting that I restart my research since they wanted to convince people that I am making up all of this thing about altering the programs since I no longer want to share my research with friends. I resisted and asked them to not alter the older programs and let me run them properly but they would not agree to it.
I want to tell friends that I absolutely love sharing my programs with friends because when all doors were closed on me, I was still able to find an expression for myself in a good way with my research and sharing it with friends. I would like to have some meanings and purpose of myself in a good way that contributes to society.
But living without my work and without programming and I have started to have pangs of depression over past few days when I stopped my programming work and it is very difficult therefore I have decided to restart my work and hope that they do not alter my new functions. This is despite that they have not allowed me to run many old functions properly.
Re: Breakthrough in the theory of stochastic differential equations and their simulation
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I was able to get my programs to work. I think many friends would already have run the good programs but, in case you have not, I am quickly posting the new versions of the main functions.
.
.
.
.
.
.
.
.
.
.
.
Here are the last few values when you run the main function.
YCoeffHH =
Columns 1 through 3
0 0 0.000000000000000
0.516150291626474 0.210155659504569 -0.002249247186387
0.079886307131609 0.038320722781206 -0.002914685934181
0.014238229495272 -0.005353846231259 -0.000206320558813
0.000582731628418 -0.000309388774534 -0.000049159883874
0.000885327028014 -0.000182860240725 -0.000045718758627
Columns 4 through 6
0 -0.000000000000000 -0.000000000000000
-0.000155390728398 -0.000514122151043 -0.000113510464299
-0.000102119083533 0.000024786488846 0.000012477074948
-0.000141263999664 -0.000037284412828 0.000003177506830
-0.000036100289804 -0.000005880156932 -0.000000606560238
-0.000009122837943 0.000000032256551 0.000000316430970
Look at output oof 2D Hermite-Series
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
YMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016162396242489 0.036215193260982
Columns 4 through 6
0.104307158908803 0.367014216578896 1.523776700116779
Look at comparison of second moments/moments
IndexMax =
201
YMomentsModel =
1.0e+02 *
Columns 1 through 3
0.017409823993282 0.036940044638198 0.092703856184305
Columns 4 through 6
0.269533422669167 0.895462482565601 3.370955049163986
DataMoments =
1.0e+02 *
Columns 1 through 3
0.017500827783291 0.037006085169492 0.091488739766061
Columns 4 through 6
0.258136573740686 0.815135310459562 2.833876685202050
Look at comparison of moments
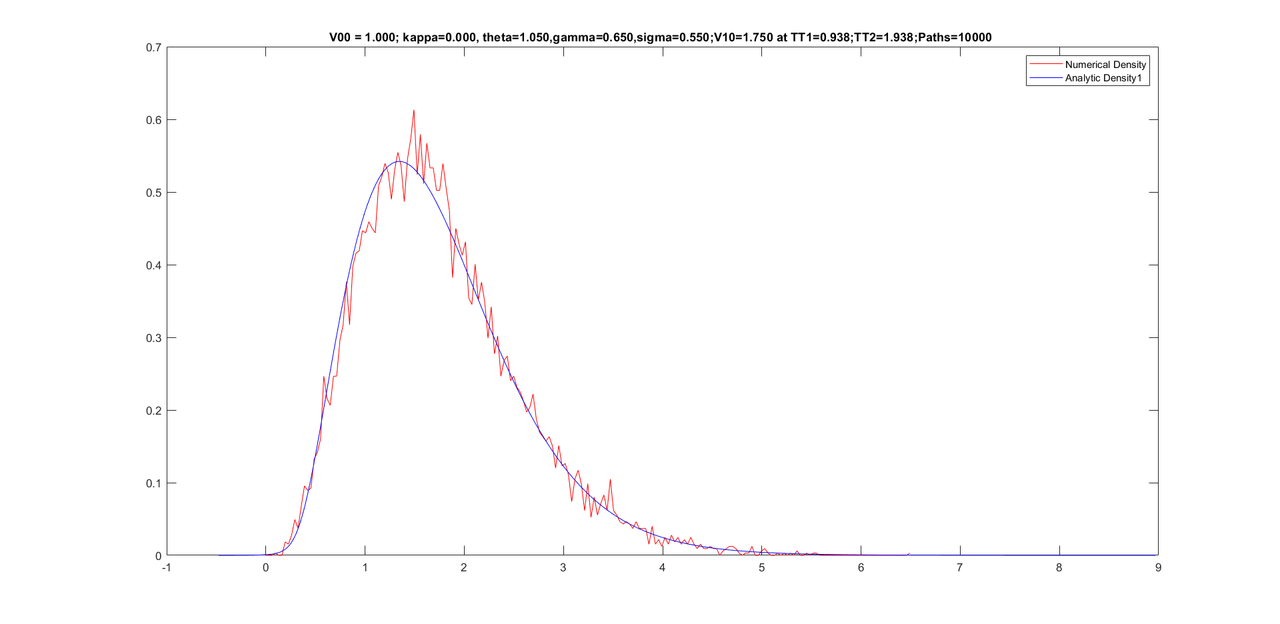
Look at density
This is the first version without altering the moments of conditional density
Here is the graph you see when you run the function.
.
.
.
.
.
.
Code: Select all
function []= ConditionalDensityHermitesBivariateNewtonItersRegSqr02()
%SV SDE is
%dV(t)=mu1 V(t)^beta1 dt+ mu2 V(t)^beta2 dt + sigma0 V(t)^gamma dZ(t)
%In mean reverting SDEs we ususally have
%mu1= kappaV * thetaV
%beta1=0
%mu2=-kappa
%beta2=0
Order=5;
%NDim=4;%Three assets and one SV.
NMomentsY=Order+1;
NMomentsX=Order+1;
w2D0(1:NMomentsY,1:NMomentsX)=1;
w2D5(1:NMomentsY,1:NMomentsX)=1;
w2D6(1:NMomentsY,1:NMomentsX)=1;
for nn=NMomentsY-1:-1:1
for mm=NMomentsX-1:-1:1
w2D5(nn,mm)=w2D5(nn+1,mm+1)*(nn+1).^5*(mm+1).^5.0;
w2D6(nn,mm)=w2D6(nn+1,mm+1)*(nn+1).^6*(mm+1).^6.0;
end
end
w2D0(1:NMomentsY,1:NMomentsX)=1;
w2Dh(1:NMomentsY,1:NMomentsX)=1;
w2D1(1:NMomentsY,1:NMomentsX)=1;
w2D2(1:NMomentsY,1:NMomentsX)=1;
w2D3(1:NMomentsY,1:NMomentsX)=1;
w2D4(1:NMomentsY,1:NMomentsX)=1;
for nn=NMomentsY-1:-1:1
for mm=NMomentsX-1:-1:1
w2Dh(nn,mm)=w2Dh(nn+1,mm+1)*(nn+1).^.5*(mm+1).^.5;
w2D1(nn,mm)=w2D1(nn+1,mm+1)*(nn+1)*(mm+1);
w2D2(nn,mm)=w2D2(nn+1,mm+1)*(nn+1).^2*(mm+1).^2.0;
w2D3(nn,mm)=w2D3(nn+1,mm+1)*(nn+1).^3*(mm+1).^3.0;
w2D4(nn,mm)=w2D4(nn+1,mm+1)*(nn+1).^4*(mm+1).^4.0;
end
end
%%%%%%%%%%%%%%%%%%%5
%%%%%%%%%%%%%%%%%%%5
V0=1.00;%.32;
V00=V0;
thetaV=1.050;%.045;%1;%.04;
kappaV=.000;%1.5;%1.5;
mu1=kappaV*thetaV;
mu2=-kappaV;
beta1=0;
beta2=1;
%gamma=.5;%.950;
%sigma0=.55;%.45;%
gamma=.65;%.950;.55
sigma0=.55;%.45;%.65
dt=.03125/2;
Tt=64*2;
T=Tt*dt;
seed0=52130649;
seed0=94210876;
rng(seed0, 'twister')
paths=10000;
V(1:paths,1)=V0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
TT1=60; %Transition distribution start
TT2=124; %Transition distribution end
Random2(1:paths/2,1)=0;
for tt=1:Tt
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
if(tt==TT1)
Xin(1:paths,1)=V(1:paths,1);
end
if(tt==TT2)
Yin(1:paths,1)=V(1:paths,1);
end
end
str=input("I have reached stone 1");
Order=5;
%
Ndata=paths;
%
[ZI] = MomentMatchedStandardNormalDiscretizedDensity(Ndata);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%55
[XCoeffH,Zx] = CalculateHermiteSeriesFromData01(Xin,Order,ZI);
[XCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(XCoeffH(1:Order+1),Order);
for qq1=1:Order+1
XMoments(qq1)=sum(Xin(1:paths).^qq1)/paths;
end
[XCoeffZ(1),XCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(XMoments,XCoeffZ(2:6));
[XCoeffH] = ConvertZSeriesToHermiteSeriesNew(XCoeffZ,Order);
for nn=1:paths
[Zx(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Xin(nn),XCoeffZ(1),XCoeffZ(2:6));
end
Zx0(1:Ndata,1)=Zx(1:Ndata);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[YCoeffH,Zy] = CalculateHermiteSeriesFromData01(Yin,Order,ZI);
[YCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffH(1:Order+1),Order);
for pp1=1:Order+1
YMoments(pp1)=sum(Yin(1:paths).^pp1)/paths;
end
[YCoeffZ(1),YCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YMoments,YCoeffZ(2:6));
%[YCoeffZ(1),YCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMoments02(YMoments);
[YCoeffH0] = ConvertZSeriesToHermiteSeriesNew(YCoeffZ,Order);
for nn=1:paths
[Zy(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Yin(nn),YCoeffZ(1),YCoeffZ(2:6));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
HH=5;
[CorrH] = CalculateCorrelationBivariateHermiteCH0(Zx,Zy,paths,HH)
CorrH
str=input("Look at hermites correlation");
Coeffyx2(1)=YCoeffH0(1);
Coeffyx2(2:6)=CorrH(1:5).*YCoeffH0(2:6);
Ydecorr(1:Ndata,1)=Yin(1:Ndata,1)-Coeffyx2(1) ...
-Coeffyx2(2).*Zx0(1:Ndata,1) ...
-Coeffyx2(3).*(Zx0(1:Ndata,1).^2-1) ...
-Coeffyx2(4).*(Zx0(1:Ndata,1).^3-3*Zx0(1:Ndata,1)) ...
-Coeffyx2(5).*(Zx0(1:Ndata,1).^4-6*Zx0(1:Ndata,1).^2+3) ...
-Coeffyx2(6).*(Zx0(1:Ndata,1).^5-10*Zx0(1:Ndata,1).^3+15*Zx0(1:Ndata,1));% ...
%-Coeffyx2(7).*(Zx0(1:Ndata,1).^6-15*Zx0(1:Ndata,1).^4+45*Zx0(1:Ndata,1).^2-15) ...
%-Coeffyx2(8).*(Zx0(1:Ndata,1).^7-21*Zx0(1:Ndata,1).^5+105*Zx0(1:Ndata,1).^3-105*Zx0(1:Ndata,1));% ...
clf;
Coeffyx2
PlotHermiteSeriesDensityAndRvGraph(Coeffyx2(1),Coeffyx2(2:Order+1),'b')
str=input("Look at initial correlated hermite series plot---2");
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[YdCoeffH,Zyd] = CalculateHermiteSeriesFromData01(Ydecorr,Order,ZI);
[YdCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YdCoeffH(1:Order+1),Order);
for pp1=1:Order+1
YdecorrMoments(pp1,1)=sum(Ydecorr(1:paths).^pp1)/paths;
end
[YdCoeffZ(1),YdCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YdecorrMoments,YdCoeffZ(2:6));
%[YdCoeffZ(1),YdCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMoments02(YdecorrMoments);
[YdCoeffH] = ConvertZSeriesToHermiteSeriesNew(YdCoeffZ,Order);
clf;
PlotHermiteSeriesDensityAndRvGraph(YdCoeffH(1),YdCoeffH(2:Order+1),'b')
str=input("Look at YdCoeffH density");
for nn=1:paths
[Zyd(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Ydecorr(nn),YdCoeffZ(1),YdCoeffZ(2:6));
end
Zyd0(1:paths,1)=Zyd(1:paths);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
YCoeffHH(1:6,1:6)=0.0;
YCoeffHH(2:6,1)=YdCoeffH(1,2:6);%*XCoeffRatio(1);
YCoeffHH
str=input("Look at 2D Hermite-series---5");
%%%%%%%%%%%%%%%%%%%%%%%%%%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YCoeffZ,MaxIter,w2D)
for pp1=1:Order+1
for qq1=1:Order+1
MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Ydecorr(1:paths,1).^pp1.*Xin(1:paths,1).^qq1)/paths;
%MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Ydecorr(1:paths,1).^pp1.*Zx0(1:paths,1).^qq1)/paths;
%MomentsYX(pp1,qq1)=sum((1:paths,1).^pp1.*Zx0(1:paths,1).^qq1)/paths;
end
end
% MomentsYX
% str=input("Look at cross-moments matrix");
MaxIter=150;
%In the function below, we do iterative optimization on all 2D Hermite
%coefficients excluding the first row. This function is applied when we
%have become too close to the true values by optimization through previous
%function.
%ZCoeffZ(1:6)=0;
%ZCoeffZ(2)=1;
%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D2);
%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd04(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D2);
%YCoeffHH
TargetCrossMoments=MomentsYX0;
OrderY=Order;
OrderX=Order;
%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd04(YCoeffHH,XCoeffZ,TargetCrossMoments,YdCoeffH,OrderY,OrderX,MaxIter);
MaxIter=1000;
[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D2);
% YObs(1:paths,1)=Ydecorr(1:paths,1);
% XObs(1:paths,1)=Xin(1:paths);
% %Zx0(1:paths,1)
% %Zyd(1:paths,1)
% XCoeffH0(1:Order+1,1)=XCoeffH(1:Order+1);
% %YdCoeffH(1:Order+1)
%
% [YCoeffHH,ObjFunc] = HSeriesCoeffsFromDataIterative2DDataA(YObs,XObs,YCoeffHH,XCoeffH0,Zx0,Zyd,YdCoeffH,MaxIter,Order,Ndata);
% %[ObjFuncBest] = Calculate2DObjWithData(YObs,XObs,YCoeffHH,XCoeffH,Hx,Hy,Ndata,Order);
%load("C:\Users\Lenovo\Documents\MATLAB\MATLAB1\pqfile02A.mat","YCoeffHH")%45000
YCoeffHH
str=input("Variable has been saved")
%YCoeffHH(6,:)=YCoeffHH(6,:);
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
%load("C:\Users\Lenovo\Documents\MATLAB\MATLAB1\pqfile02.mat","YCoeffZZ")%45000
MaxIter=2500;
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeriesSubset(YCoeffZZ,XCoeffZ,Order,MomentsYX0,YdecorrMoments,YdCoeffH,MaxIter);
%[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
%LG[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeries(YCoeffZZ,XCoeffZ,Order,MomentsYX0,YdecorrMoments,MaxIter);
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeriesWithData(YCoeffZZ,XCoeffZ,Order,MomentsYX0,YdecorrMoments,MaxIter);%,Zyd,Zx,Ndata);
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeriesWithData(YCoeffZZ,ZCoeff,Order,MomentsYX0,MomentsY,MaxIter,Zyd,Zx,Ndata);
%[YdecorrMomentsM] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);
%YdecorrMomentsM
%YdecorrMoments
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[YdecorrMomentsM] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);
YdecorrMomentsM
YdecorrMoments
str=input("Look at comparison of moments")
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[YCoeffHH] = ConvertZSeriesToHermiteSeries2D(YCoeffZZ,Order+1,Order+1);
YCoeffHH
str=input("Look at output oof 2D Hermite-Series");
YCoeffHH(1,1:Order+1)=YCoeffHH(1,1:Order+1)*0+Coeffyx2(1,1:Order+1);
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
[Y1DMoments]=CalculateMomentsOfZSeries(YCoeffZ(1),YCoeffZ(2:6),5,6)
OrderY=Order;
OrderX=Order;
NMoments=6;
[YMoments] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,OrderY,OrderX,NMoments);
%
%
Y1DMoments
YMoments
str=input("Look at comparison of second moments/moments");
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%In this block, we do conditional Monte Carlo of SDE which is the true
%numerical 1D conditional density of Y conditional on X having a given
%value. This value of X on which we are conditionin is defined by V10 below.
%We can alter V10 below and it will take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
%Zx=2.0;
%V10=XCoeffZ(1)+XCoeffZ(2).*Zx+XCoeffZ(3).*Zx^2+XCoeffZ(4).*Zx^3+XCoeffZ(5).*Zx^4+XCoeffZ(6).*Zx^5;
%V10
%str=input("Look at V10");
V10=1.750;
V(1:paths)=V10;
Random2(1:paths,1)=0;
for tt=TT1+1:TT2
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
end
%Below
NoOfBins=200;
MaxCutOff=10;
[XDensity,IndexOut,IndexMax] = MakeDensityFromSimulation_Infiniti_NEW(V,paths,NoOfBins,MaxCutOff );
clf;
plot(IndexOut(1:IndexMax),XDensity(1:IndexMax),'r');
hold on
for qq=1:6
DataMoments(qq)=sum(V(:).^qq)/paths;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%Below, we calculate the value of Zx0 corresponding to X0 (here V10). This
%comes from inverting the Z-series of X so that X=V10;
xOrder=Order;
yOrder=Order;
[Zx0] = CalculateZgivenXAndHSeriesCoeffs(V10,XCoeffH,xOrder);
%Below, we collapse two dimensional pdf of Y|X to one dimensional pdf given
%Zx i.e. this Y|X=X(Zx)
%Here we take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
He(1)=1;
He(2)=Zx0;
He(3)=Zx0^2-1;
He(4)=Zx0^3-3*Zx0;
He(5)=Zx0^4-6*Zx0.^2+3;
He(6)=Zx0^5-10*Zx0.^3+15*Zx0;
He(7)=Zx0^6-15*Zx0.^4+45*Zx0.^2-15;
He(8)=Zx0^7-21*Zx0.^5+105*Zx0.^3-105*Zx0;
YCoeffh(1:Order+1)=0;
for hh=1:yOrder+1
for hh2=1:xOrder+1
YCoeffh(hh)=YCoeffh(hh)+YCoeffHH(hh,hh2).*He(hh2);
end
end
[YCoeffz(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffh(1:Order+1),Order);
[YMomentsModel]=CalculateMomentsOfZSeries(YCoeffz(1),YCoeffz(2:6),5,6);
YMomentsModel
DataMoments
str=input("Look at comparison of moments");
PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh(2:yOrder+1),'b')
%hold on
%PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh1(2:yOrder+1),'g')
title(sprintf('V00 = %.3f; kappa=%.3f, theta=%.3f,gamma=%.3f,sigma=%.3f;V10=%.3f at TT1=%.3f;TT2=%.3f;Paths=%d ',V00, kappaV, thetaV,gamma,sigma0, V10,(TT1*dt),(TT2*dt),paths));%,sprintf('theta= %f', theta), sprintf('kappa = %f', kappa),sprintf('sigma = %f', sigma0),sprintf('T = %f', T));
legend({'Numerical Density','Analytic Density1'}, ...
'Location','northeast')
str=input("This is the first version without altering the moments of conditional density")
[YMoments0]=CalculateMomentsOfZSeries(YCoeffz(1),YCoeffz(2:6),5,6)
end.
.
.
Code: Select all
function [YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D)
SeriesOrder=6;
NMoments=6;
Order=5;
VarY(2:Order+1)=0.0;
for nn=2:Order+1
SD(nn)=sqrt(YCoeffHH(nn,1).^2+YCoeffHH(nn,2).^2+YCoeffHH(nn,2).^2*2+YCoeffHH(nn,4).^2*6+YCoeffHH(nn,5).^2*24+YCoeffHH(nn,6).^2*120);
if(SD(nn)>YdCoeffH(nn)*1.005)
YCoeffHH(nn,1:Order+1)=YCoeffHH(nn,1:Order+1).*(YdCoeffH(nn)./SD(nn))*1.005;
end
end
%[YdMoments]=CalculateMomentsOfZSeries(YdCoeffZ(1),YdCoeffZ(2:6),5,6);
% %Below, we calculate first and 2nd moment of 2D Hermite series
% [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHH,Order,Order);
% %VarHH is model variance .
% VarHH=M2HH-MeanHH.^2;
% %VarIn is input variance
% VarIn=YMoments(2)-YMoments(1).^2;
% %Variance correction is applied below to all rows but not to first row of hermite series.
% %YCoeffHH(2:6,1:6)=YCoeffHH(2:6,1:6).*sqrt(VarIn/VarHH);
% %YCoeffHH(1,2:6)=YCoeffHH(1,2:6).*sqrt(VarIn/VarHH);
% %We convert final 2D Hermite series to 2D Z-series
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
for nn=1:SeriesOrder
for mm=1:SeriesOrder
DeltaX(nn,mm)=.00125*2/(factorial(nn+1))/(factorial(mm+1));%/2^((nn-1)/2)/2^((mm-1)/2);
DeltaXMax(nn,mm)=DeltaX(nn,mm)*10;
end
end
ObjFunc1=0;
ObjFunc2=0;
%%%Weights on objective function that shows fit to moments
w2D(NMoments,NMoments)=1;
for nn=NMoments-1:-1:1
for mm=NMoments-1:-1:1
w2D(nn,mm)=w2D(nn+1,mm+1)*(nn+1).^0*(mm+1).^0;
end
end
[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZ,XCoeffZ,Order,Order);
[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);
for pp1=1:Order+1
for qq1=1:Order+1
Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
end
% Moments1D(pp1)=AMat((Order+1)*(Order+1)+pp1,1);
end
[ObjFuncBest] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
%ObjFuncBest=ObjFuncBest+sum((BMat-YdMoments).^2);
%[ObjFuncBest] = CalculateObjMoment(sMu,Moments,w,mOrder);
ObjFuncBest
str=input("Look objFuncBest");
%cBest=c;
ImproveFlag(1:SeriesOrder,1:SeriesOrder)=1;
ImproveFlagPrev(1:SeriesOrder,1:SeriesOrder)=0;
ImproveCount(1:SeriesOrder,1:SeriesOrder)=0;
SeriesOrderM=6;
kk=0;
while ((kk<MaxIter)&&(ObjFuncBest>.001))
kk=kk+1;
%We only iteratively alter c(2:7), first and second moments are
%retrieved automatically in our set up
for nn=2:6%SeriesOrder
for mm=1:6%SeriesOrder
if((nn==1))
% ;
else
ImproveFlagPrev(nn,mm)=ImproveFlag(nn,mm);
YCoeffHHnew=YCoeffHH;
YCoeffHHnew(nn,mm)=YCoeffHHnew(nn,mm)+DeltaX(nn,mm);
YSD(nn)=sqrt(YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,3).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120);
if(YSD(nn)>abs(YdCoeffH(nn))*1.005)
YCoeffHHnew(nn,:)=YCoeffHHnew(nn,:).*abs(YdCoeffH(nn))./YSD(nn)*1.005;
end
%
% if(nn>1)
% VarY(nn)=YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,2).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120;
% if(VarY(nn)>1.15^2*YdCoeffH(nn).^2)
% YCoeffHHnew(nn,1:Order+1)=YCoeffHHnew(nn,1:Order+1).*sqrt(YdCoeffH(nn).^2./VarY(nn))*1.15;
% end
% end
%Below, we calculate first and 2nd moment of 2D Hermite series
% [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHHnew,Order,Order);
%VarHH is model variance .
% VarHH=M2HH-MeanHH.^2;
%VarIn is input variance
% VarIn=YMoments(2)-YMoments(1).^2;
%Variance correction is applied below to all rows but not to first row of hermite series.
% YCoeffHHnew(2:6,1:6)=YCoeffHHnew(2:6,1:6).*sqrt(VarIn/VarHH);
% YCoeffHHnew(1,2:6)=YCoeffHHnew(1,2:6).*sqrt(VarIn/VarHH);
%We convert final 2D Hermite series to 2D Z-series
[YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
for pp1=1:Order+1
for qq1=1:Order+1
Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
end
end
[ObjFunc1] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZnew,Order,Order,Order+1);
%ObjFunc1=ObjFunc1+sum((BMat-YdMoments).^2);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.0,Order);
DFlag1=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.0,Order);
DFlag2=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
%DValue1=1;
%DValue2=1;
%DFlag1=1;
%DFlag2=1;
if((ObjFunc1<ObjFuncBest)&&(DFlag1==1)&&(DFlag2==1))
%if(ObjFunc1<ObjFuncBest)
ObjFuncBest=ObjFunc1;
YCoeffHH=YCoeffHHnew;
ImproveFlag(nn,mm)=1;
else
YCoeffHHnew=YCoeffHH;
YCoeffHHnew(nn,mm)=YCoeffHHnew(nn,mm)-DeltaX(nn,mm);
%
% YSD(nn)=sqrt(YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,3).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120);
%
if(YSD(nn)>abs(YdCoeffH(nn))*1.005)
YCoeffHHnew(nn,:)=YCoeffHHnew(nn,:).*abs(YdCoeffH(nn))./YSD(nn)*1.005;
end
%
% if(nn>1)
% VarY(nn)=YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,2).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120;
% if(VarY(nn)>1.15^2*YdCoeffH(nn).^2)
% YCoeffHHnew(nn,1:Order+1)=YCoeffHHnew(nn,1:Order+1).*sqrt(YdCoeffH(nn).^2./VarY(nn))*1.15;
% end
% end
%Below, we calculate first and 2nd moment of 2D Hermite series
% [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHHnew,Order,Order);
%VarHH is model variance .
% VarHH=M2HH-MeanHH.^2;
%VarIn is input variance
% VarIn=YMoments(2)-YMoments(1).^2;
%Variance correction is applied below to all rows but not to first row of hermite series.
% YCoeffHHnew(2:6,1:6)=YCoeffHHnew(2:6,1:6).*sqrt(VarIn/VarHH);
% YCoeffHHnew(1,2:6)=YCoeffHHnew(1,2:6).*sqrt(VarIn/VarHH);
%We convert final 2D Hermite series to 2D Z-series
[YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
for pp1=1:Order+1
for qq1=1:Order+1
Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
end
end
[ObjFunc2] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZnew,Order,Order,Order+1);
% ObjFunc2=ObjFunc2+sum((BMat-YdMoments).^2);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,-3.0,2.0,Order);
DFlag1=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
[DValue1] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-3.0,Order);
[DValue2] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,3.0,Order);
[DValue3] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.5,Order);
[DValue4] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.5,Order);
[DValue5] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,-2.0,Order);
[DValue6] = EvaluateDerivativeOf2DZSeries(YCoeffZZnew,3.0,2.0,Order);
DFlag2=(DValue1>0)&&(DValue2>0)&&(DValue3>0)&&(DValue4>0)&&(DValue5>0)&&(DValue6>0);
%DValue1=1;
%DValue2=1;
%DFlag1=1;
%DFlag2=1;
if((ObjFunc2<ObjFuncBest)&&(DFlag1==1)&&(DFlag2==1))
% if(ObjFunc2<ObjFuncBest)
ObjFuncBest=ObjFunc2;
YCoeffHH=YCoeffHHnew;
ImproveFlag(nn,mm)=-1;
else
ImproveFlag(nn,mm)=0;
end
end
end
end
end
if(rem(kk,1)==0)
kk
ObjFunc1
ObjFunc2
ObjFuncBest
YCoeffHH
ImproveCount
end
ImproveFlag0=0;
for nn=1:SeriesOrder
for mm=1:SeriesOrder
if(ImproveFlag(nn,mm)==0)
DeltaX(nn,mm)=DeltaX(nn,mm)*.88;
%ImproveFlag0=1;
end
if((ImproveFlag(nn,mm)==1)||(ImproveFlag(nn,mm)==-1))
DeltaX(nn,mm)=DeltaX(nn,mm)*1.1;
%ImproveFlag0=1;
end
if(DeltaX(nn,mm)>DeltaXMax(nn,mm))
DeltaX(nn,mm)=DeltaXMax(nn,mm);
end
end
end
end
ObjFunc=ObjFuncBest;
end.
.
Here are the last few values when you run the main function.
YCoeffHH =
Columns 1 through 3
0 0 0.000000000000000
0.516150291626474 0.210155659504569 -0.002249247186387
0.079886307131609 0.038320722781206 -0.002914685934181
0.014238229495272 -0.005353846231259 -0.000206320558813
0.000582731628418 -0.000309388774534 -0.000049159883874
0.000885327028014 -0.000182860240725 -0.000045718758627
Columns 4 through 6
0 -0.000000000000000 -0.000000000000000
-0.000155390728398 -0.000514122151043 -0.000113510464299
-0.000102119083533 0.000024786488846 0.000012477074948
-0.000141263999664 -0.000037284412828 0.000003177506830
-0.000036100289804 -0.000005880156932 -0.000000606560238
-0.000009122837943 0.000000032256551 0.000000316430970
Look at output oof 2D Hermite-Series
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
Y1DMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016205788621208 0.036425787242405
Columns 4 through 6
0.106054113503100 0.383029718968561 1.660423202870474
YMoments =
1.0e+02 *
Columns 1 through 3
0.009995635585273 0.016162396242489 0.036215193260982
Columns 4 through 6
0.104307158908803 0.367014216578896 1.523776700116779
Look at comparison of second moments/moments
IndexMax =
201
YMomentsModel =
1.0e+02 *
Columns 1 through 3
0.017409823993282 0.036940044638198 0.092703856184305
Columns 4 through 6
0.269533422669167 0.895462482565601 3.370955049163986
DataMoments =
1.0e+02 *
Columns 1 through 3
0.017500827783291 0.037006085169492 0.091488739766061
Columns 4 through 6
0.258136573740686 0.815135310459562 2.833876685202050
Look at comparison of moments
Look at density
This is the first version without altering the moments of conditional density
Here is the graph you see when you run the function.
.
.

You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, in next 2-3 days, I want to write a more general function that is also better from the programming practices perspective and also faster and can also calibrate a 8 X 8 2D Hermite series. I hope that everything goes well and I would love to post a better and more general version of the program. I wanted to do it 7-10 days ago but got bogged down by the other problems. I hope that things remain better now.
The volatility regime in the program of last post is about the maximum you can do with a 6X6 2D Hermite series and for more volatility, we would have to use a 8X8 2D Hermite series.
The volatility regime in the program of last post is about the maximum you can do with a 6X6 2D Hermite series and for more volatility, we would have to use a 8X8 2D Hermite series.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, with a reasonable framework for calibrating coefficients of 6X6 Hermite series, we have reached a new stone in our research effort. I really think that moments and cross-moments are rather under-emphasized in our education, understanding and applications of probability theory and they can be far more useful than we currently make them.
It has been more than four years since I started working with Hermite polynomials in one dimensional probability theory. And it is very exciting to know that now we are starting to use them for two dimensions and soon we would be moving on to multiple dimensions. Even if we could do basic programs with calibration of multi-dimensional Hermite-series this year, it will take us many many years of research work to be able to fully understand and exploit the potential of multi-dimensional hermite-polynomial Series.
I know I always say it but this is exactly true that none of my work in past four years and earlier would have been possible if it were not for support of good people that sharply decreased my mind control and enabled me to work in a better way. Any success I have in solution of mathematical problems in recent years, I owe it to support from a lot of good American people. I am very thankful to them and want to request them to please continue their support. And I would like to take this opportunity to tell everyone that I have absolutely nothing against American people and I would want America to be a roaring nation when it comes to wealth and prosperity and I would want Americans to be nicest people with each other and with people of rest of the world(As most of them already are). As Reagan once said (in different words) that America is epitome of human civilization and I fully agree with that. And again if good American people had not supported me, I had no future.
And there is a long way to go and a lot of things in the current research require a better understanding and many more things still need to be understood. And I hope that my research has matured enough that a lot of other more intelligent people would like to take interest in many relevant ideas and I hope that there would be a better understanding of many related problems. And I would love to continue my research and I hope that my misery ends and I am allowed to work in a more natural environment without any coercion or problems.
I also want to take this opportunity to request all friends to please ask the American Government to end my mind control and let me live a full free life. I am already 52 and it is very difficult to live with mind control when you start to grow more old.
It has been more than four years since I started working with Hermite polynomials in one dimensional probability theory. And it is very exciting to know that now we are starting to use them for two dimensions and soon we would be moving on to multiple dimensions. Even if we could do basic programs with calibration of multi-dimensional Hermite-series this year, it will take us many many years of research work to be able to fully understand and exploit the potential of multi-dimensional hermite-polynomial Series.
I know I always say it but this is exactly true that none of my work in past four years and earlier would have been possible if it were not for support of good people that sharply decreased my mind control and enabled me to work in a better way. Any success I have in solution of mathematical problems in recent years, I owe it to support from a lot of good American people. I am very thankful to them and want to request them to please continue their support. And I would like to take this opportunity to tell everyone that I have absolutely nothing against American people and I would want America to be a roaring nation when it comes to wealth and prosperity and I would want Americans to be nicest people with each other and with people of rest of the world(As most of them already are). As Reagan once said (in different words) that America is epitome of human civilization and I fully agree with that. And again if good American people had not supported me, I had no future.
And there is a long way to go and a lot of things in the current research require a better understanding and many more things still need to be understood. And I hope that my research has matured enough that a lot of other more intelligent people would like to take interest in many relevant ideas and I hope that there would be a better understanding of many related problems. And I would love to continue my research and I hope that my misery ends and I am allowed to work in a more natural environment without any coercion or problems.
I also want to take this opportunity to request all friends to please ask the American Government to end my mind control and let me live a full free life. I am already 52 and it is very difficult to live with mind control when you start to grow more old.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I have a strong feeling that we can find some helpful equations by taking inner product of various hermite polynomials of X with square of zero mean Ydecorr. I really think that these equations could possibly be solved somehow. I want to work out the equations tonight and will hopefully come back with equations tonight or possibly tomorrow. And then we would move to the next step if we could solve the equations in some way.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, this just does not stop. Mind control agents continue to alter my programs. Here, I like to tell friends that it was not an act of benevolence on the hands of mind control agents when I posted my previous good programs two days ago. I had made some changes in my program that they could not replicate quickly and they were forced to let my output go through. Once I ran the good program, I did not re-run it and posted it on the forum the first thing otherwise my good output would have been lost.
But mind control guy has been extremely upset after I posted my programs and he would lose his temper many times again and again in past two days. They were fully adamant to stop my research by altering my programs and had a serious setback when I was able to post the good program on forum. I really do not know what narrative bad people had about me and my programs but they were not expecting that I would post anything good.
And again mind control agents are adamant at altering the programs and their output and they do it again and again whenever I make some improvements in my program. I want to request friends to please force the American government and defense to make sure that mind control agents do not change my programs. Please help me do good research.
But mind control guy has been extremely upset after I posted my programs and he would lose his temper many times again and again in past two days. They were fully adamant to stop my research by altering my programs and had a serious setback when I was able to post the good program on forum. I really do not know what narrative bad people had about me and my programs but they were not expecting that I would post anything good.
And again mind control agents are adamant at altering the programs and their output and they do it again and again whenever I make some improvements in my program. I want to request friends to please force the American government and defense to make sure that mind control agents do not change my programs. Please help me do good research.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I had tried to think properly about the analytic equations with hermite polynomials but I could not do that at home due to too high mind control. I would continue to lose my streaks of thought and failed to think hard. Therefore, in the evening today, I decided to go to a park and think about the equations, and I was able to think properly and now I have some basic analytic equations.
I am still not writing the equations since I have to first do all the formal mathematics in mathematica and then post those equations. I really I am onto something like an alternative way to solve the equations. I think I would be able to post the equations tomorrow.
I am still not writing the equations since I have to first do all the formal mathematics in mathematica and then post those equations. I really I am onto something like an alternative way to solve the equations. I think I would be able to post the equations tomorrow.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, just a bit ago, I had opened Mathematica and also had chrome open with 15-20 tabs on it. There were no other large programs open and my computer refused to open matlab saying that there was not enough space for memory paging file. I have 8GB of RAM and 288GB of 476GB free on C: drive where programs are installed. I continued to repeatedly try to run matlab but could not do that. Then I closed Chrome and Mathematica and I was able to run matlab properly.
For past two weeks, I had been seeing all sort of problems with my computer. Many times the computer becomes unresponsive and stuck. Other times, all of a sudden out of nowhere, a black screen will appear during my running of programs and then after a second or two my own screen will re-appear. Sometimes cursor will continue to move but everything would become unresponsive.
It seems to me that they continue to add more and more of there spying and other (programs that alter output of my matlab programs) programs on my computer after every few days.
Friends, I really need help since mind control agencies are very resolute to continue my mind control and they want to thwart my research at all cost.
For past two weeks, I had been seeing all sort of problems with my computer. Many times the computer becomes unresponsive and stuck. Other times, all of a sudden out of nowhere, a black screen will appear during my running of programs and then after a second or two my own screen will re-appear. Sometimes cursor will continue to move but everything would become unresponsive.
It seems to me that they continue to add more and more of there spying and other (programs that alter output of my matlab programs) programs on my computer after every few days.
Friends, I really need help since mind control agencies are very resolute to continue my mind control and they want to thwart my research at all cost.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I did some analysis using mathematica. I have some limited success. Basically we can get up to ten extra equations from inner product of various hermite polynomials with square of bivariate Hermite-series Variable X. It is not enough to pin down any variable but might be usable as extra constraints in our iterative method or as extra constraints in Newton method. I have to further see it but would post a more technical note about it tomorrow.
I had been given a Fluanxol injection on 18th Nov and week after the injection is when the effect of injection is highest and difficult to do any solid work. And that has been the reason behind slow speed of work. I hope I will be far better in a week when the effect of injection recedes.
I had been given a Fluanxol injection on 18th Nov and week after the injection is when the effect of injection is highest and difficult to do any solid work. And that has been the reason behind slow speed of work. I hope I will be far better in a week when the effect of injection recedes.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
we have to calibrate 2D Hermite-series of \(\left[Y|X\right]\) which is of the form
\begin{align}
\left[Y|X\right](Z_y \, , \, Z_x)\, \,&=\, \Big[\, b_{0,0} \, + \, b_{0,1} \,H_1(Z_x) \,+\, b_{0,2} \, H_2(Z_x) \,\, + \, b_{0,3} \,H_3(Z_x)\,\,+\,\ldots\,\Big] \\
&+\, \Big[ \, b_{1,0} \, + \, b_{1,1} \,H_1(Z_x) \,+\, b_{1,2} \, H_2(Z_x) \, + \, b_{1,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_1(Z_y) \, \\
&+\, \Big[ \, b_{2,0} \, + \, b_{2,1} \,H_1(Z_x) \,+\, b_{2,2} \, H_2(Z_x) \, \, + \, b_{2,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_2(Z_y) \, \\
&+\,\,\,\ldots\, \\
\end{align}
Even though one dimensional regression worked reasonably to calculate the coefficients of Hermite-Series, when we tried to calculate coefficients of 2D Hermite-Series with regression, it did not work well because it is difficult to catch correlations in variance using first order variables especially when there is double stochasticity.
I suggest the we remove the 1st order correlation effect of X on Y and write Zero mean Ydecorr as
\begin{align}
\left[Ydecorr|X\right](\tilde{Z}_y \, , \, Z_x)\, \,&=\, \, \Big[ \, b_{1,0} \, + \, b_{1,1} \,H_1(Z_x) \,+\, b_{1,2} \, H_2(Z_x) \, + \, b_{1,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \,H_1(\tilde{Z}_y) \, \\
&+\, \Big[ \, b_{2,0} \, + \, b_{2,1} \,H_1(Z_x) \,+\, b_{2,2} \, H_2(Z_x) \, \, + \, b_{2,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_2(\tilde{Z}_y) \, \\
&+\, \Big[ \, b_{3,0} \, + \, b_{3,1} \,H_1(Z_x) \,+\, b_{3,2} \, H_2(Z_x) \, \, + \, b_{3,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_3(\tilde{Z}_y) \, \\
&+\,\,\,\ldots\, \\
\end{align}
I suggest that we do a regression of \(Ydecorr\) on squared hermite polynomials since we know the formula
\begin{align}
\left[{Ydecorr}^2|X\right](\tilde{Z}_y \, , \, Z_x)\, \,&=\, \, \Big[ \, {b_{1,0}}^2 \, + \, {b_{1,1}}^2 \,{H_1(Z_x)}^2 \,+\, {b_{1,2}}^2 \, {H_2(Z_x)}^2 \, + \, {b_{1,3}}^2 \,{H_3(Z_x)}^2\,\,+\,\ldots\, \Big] \,{H_1(\tilde{Z}_y)}^2 \, \\
&+\, \Big[ \, {b_{2,0}}^2 \, + \, {b_{2,1}}^2 \,{H_1(Z_x)}^2 \,+\, {b_{2,2}}^2 \, {H_2(Z_x)}^2 \, + \, {b_{2,3}}^2 \,{H_3(Z_x)}^2\,\,+\,\ldots\, \Big] \,{H_2(\tilde{Z}_y)}^2 \, \\
&+\, \Big[ \, {b_{3,0}}^2 \, + \, {b_{3,1}}^2 \,{H_1(Z_x)}^2 \,+\, {b_{3,2}}^2 \, {H_2(Z_x)}^2 \, + \, {b_{3,3}}^2 \,{H_3(Z_x)}^2\,\,+\,\ldots\, \Big] \,{H_3(\tilde{Z}_y)}^2 \, \\
&+\,\,\,\ldots\, \\
\end{align}
If we do a regression as above, we will get squared coefficients of 2D Hermite-series as a result of least squares regression of Ydecorr on squared values of underlying hermite polynomials. We will have to convert the squared values of coefficients to first power by taking square-root and then apply an appropriate sign from information elsewhere.
We know that above is a true equation and if we take expectations on right side on squared hermite polynomials, we would get the second moment of the variable underlying hermite series on the left.
I am trying to do this and hope that my programs are not altered and hope to make a new post with results later tonight.
\begin{align}
\left[Y|X\right](Z_y \, , \, Z_x)\, \,&=\, \Big[\, b_{0,0} \, + \, b_{0,1} \,H_1(Z_x) \,+\, b_{0,2} \, H_2(Z_x) \,\, + \, b_{0,3} \,H_3(Z_x)\,\,+\,\ldots\,\Big] \\
&+\, \Big[ \, b_{1,0} \, + \, b_{1,1} \,H_1(Z_x) \,+\, b_{1,2} \, H_2(Z_x) \, + \, b_{1,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_1(Z_y) \, \\
&+\, \Big[ \, b_{2,0} \, + \, b_{2,1} \,H_1(Z_x) \,+\, b_{2,2} \, H_2(Z_x) \, \, + \, b_{2,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_2(Z_y) \, \\
&+\,\,\,\ldots\, \\
\end{align}
Even though one dimensional regression worked reasonably to calculate the coefficients of Hermite-Series, when we tried to calculate coefficients of 2D Hermite-Series with regression, it did not work well because it is difficult to catch correlations in variance using first order variables especially when there is double stochasticity.
I suggest the we remove the 1st order correlation effect of X on Y and write Zero mean Ydecorr as
\begin{align}
\left[Ydecorr|X\right](\tilde{Z}_y \, , \, Z_x)\, \,&=\, \, \Big[ \, b_{1,0} \, + \, b_{1,1} \,H_1(Z_x) \,+\, b_{1,2} \, H_2(Z_x) \, + \, b_{1,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \,H_1(\tilde{Z}_y) \, \\
&+\, \Big[ \, b_{2,0} \, + \, b_{2,1} \,H_1(Z_x) \,+\, b_{2,2} \, H_2(Z_x) \, \, + \, b_{2,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_2(\tilde{Z}_y) \, \\
&+\, \Big[ \, b_{3,0} \, + \, b_{3,1} \,H_1(Z_x) \,+\, b_{3,2} \, H_2(Z_x) \, \, + \, b_{3,3} \,H_3(Z_x)\,\,+\,\ldots\, \Big] \, H_3(\tilde{Z}_y) \, \\
&+\,\,\,\ldots\, \\
\end{align}
I suggest that we do a regression of \(Ydecorr\) on squared hermite polynomials since we know the formula
\begin{align}
\left[{Ydecorr}^2|X\right](\tilde{Z}_y \, , \, Z_x)\, \,&=\, \, \Big[ \, {b_{1,0}}^2 \, + \, {b_{1,1}}^2 \,{H_1(Z_x)}^2 \,+\, {b_{1,2}}^2 \, {H_2(Z_x)}^2 \, + \, {b_{1,3}}^2 \,{H_3(Z_x)}^2\,\,+\,\ldots\, \Big] \,{H_1(\tilde{Z}_y)}^2 \, \\
&+\, \Big[ \, {b_{2,0}}^2 \, + \, {b_{2,1}}^2 \,{H_1(Z_x)}^2 \,+\, {b_{2,2}}^2 \, {H_2(Z_x)}^2 \, + \, {b_{2,3}}^2 \,{H_3(Z_x)}^2\,\,+\,\ldots\, \Big] \,{H_2(\tilde{Z}_y)}^2 \, \\
&+\, \Big[ \, {b_{3,0}}^2 \, + \, {b_{3,1}}^2 \,{H_1(Z_x)}^2 \,+\, {b_{3,2}}^2 \, {H_2(Z_x)}^2 \, + \, {b_{3,3}}^2 \,{H_3(Z_x)}^2\,\,+\,\ldots\, \Big] \,{H_3(\tilde{Z}_y)}^2 \, \\
&+\,\,\,\ldots\, \\
\end{align}
If we do a regression as above, we will get squared coefficients of 2D Hermite-series as a result of least squares regression of Ydecorr on squared values of underlying hermite polynomials. We will have to convert the squared values of coefficients to first power by taking square-root and then apply an appropriate sign from information elsewhere.
We know that above is a true equation and if we take expectations on right side on squared hermite polynomials, we would get the second moment of the variable underlying hermite series on the left.
I am trying to do this and hope that my programs are not altered and hope to make a new post with results later tonight.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, it does not seem to work properly as suggested in previous post. There are many negative coefficients when all coefficients should be positive. And there are other problems. Also very sensitive to order of regression variables. Trailing coefficients seem to be way too large. etc.
I am trying to remain in the previous set up of iterative method. May be try some sort of multi-level method that gets 4X4 matrix of coefficients to easily work and project it on 6X6 matrix of coefficients and then project it on 8X8 matrix of coefficients.
I am trying to remain in the previous set up of iterative method. May be try some sort of multi-level method that gets 4X4 matrix of coefficients to easily work and project it on 6X6 matrix of coefficients and then project it on 8X8 matrix of coefficients.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
