Friends, I want to make a general version of the previous program that can take non-square cross-moments matrix and can also work till at least eighth moment. It can take a day or two. I want to keep the program general.
Then I will take 2-3 days to sum up and explain with latex equations everything that we have been doing since past one week including the later work.
I also thought about properties of moments so that resulting calibrated Z-series would have proper tails. Suppose moment(n) is nth central moment of a Z-series. I tried that ratio moment(6)/moment(5) has to be equal to or greater than the ratio moment(4)/moment(3). Please note that these moments are central. I tried it on a few Z-series and it seemed to work and the tail would become proper and accurate but it was very initial and I need more work to see if it always holds. In general, I would suggest when there are eight moments then (we take absolute values of moments in case of negative odd moments)
moment(8)/moment(7) >= moment (6)/moment(5) >=moment(4)/moment(3)
where all of the above are central moments. At the moment, this is just suggestive and I need more work to verify this.
I hope to share interesting work in coming days.
Re: Breakthrough in the theory of stochastic differential equations and their simulation
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, for the calculations of model cross-moments, I have been using the Hermite-series of independent variable X derived from least squares regression. Just like its two dimensional counterpart, this one dimensional Z-series/Hermite-Series have enough noise in its highest coefficients associated with higher hermite polynomials when derived from regression. The noise in these higher coefficients contributes to instability of the whole process. I have tried finding this one dimensional density of independent variable X from fitting of moments on one dimensional Z-series and it increases the robustness of the whole process. The 1D Coefficients derived from fitting of one dimensional moments are more stable and, as a result, the two dimensional model cross-moment calculations are more well-behaved and robust. In a few hours, I will post this new matlab program for friends.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
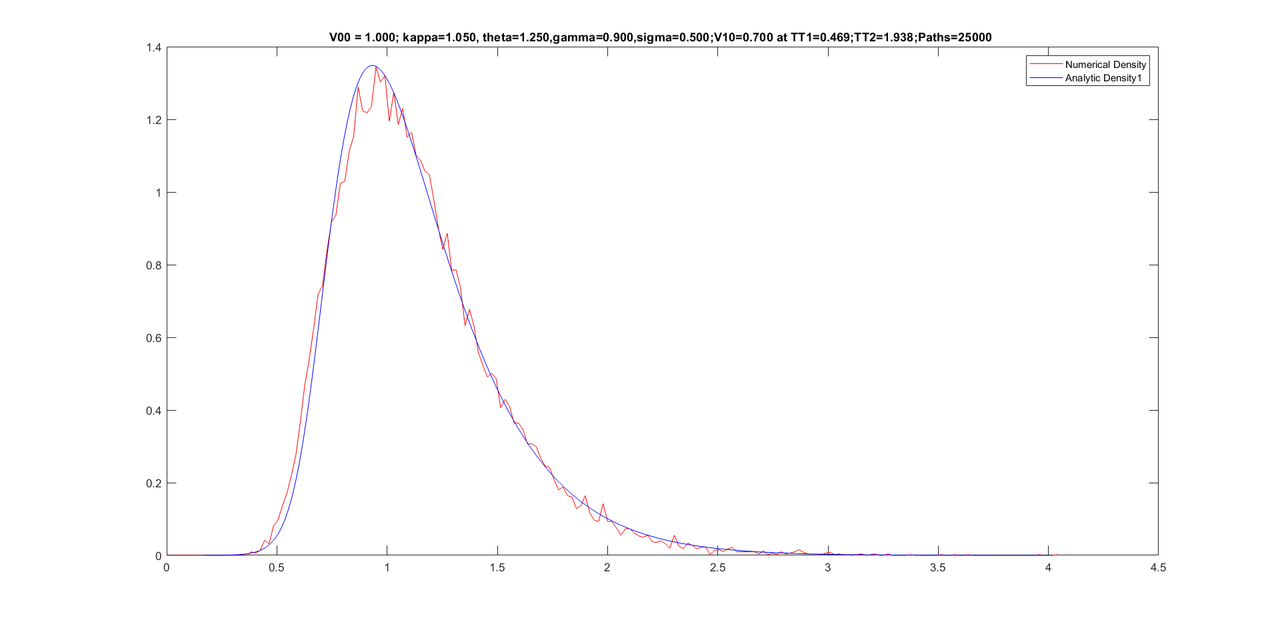
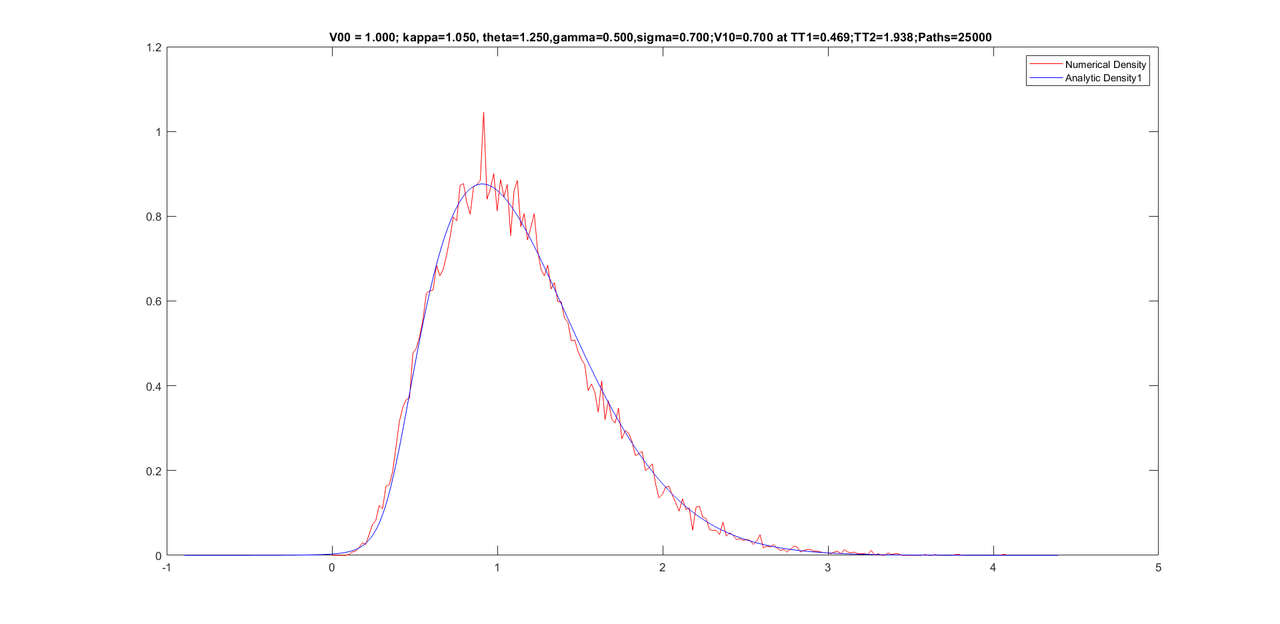
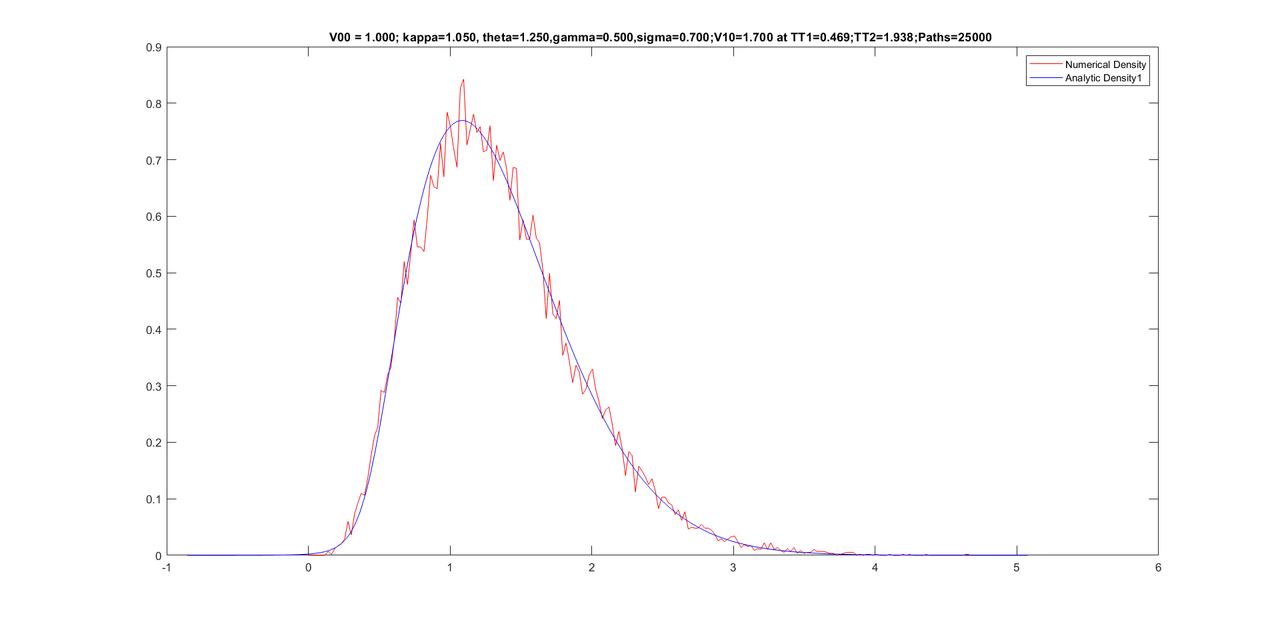
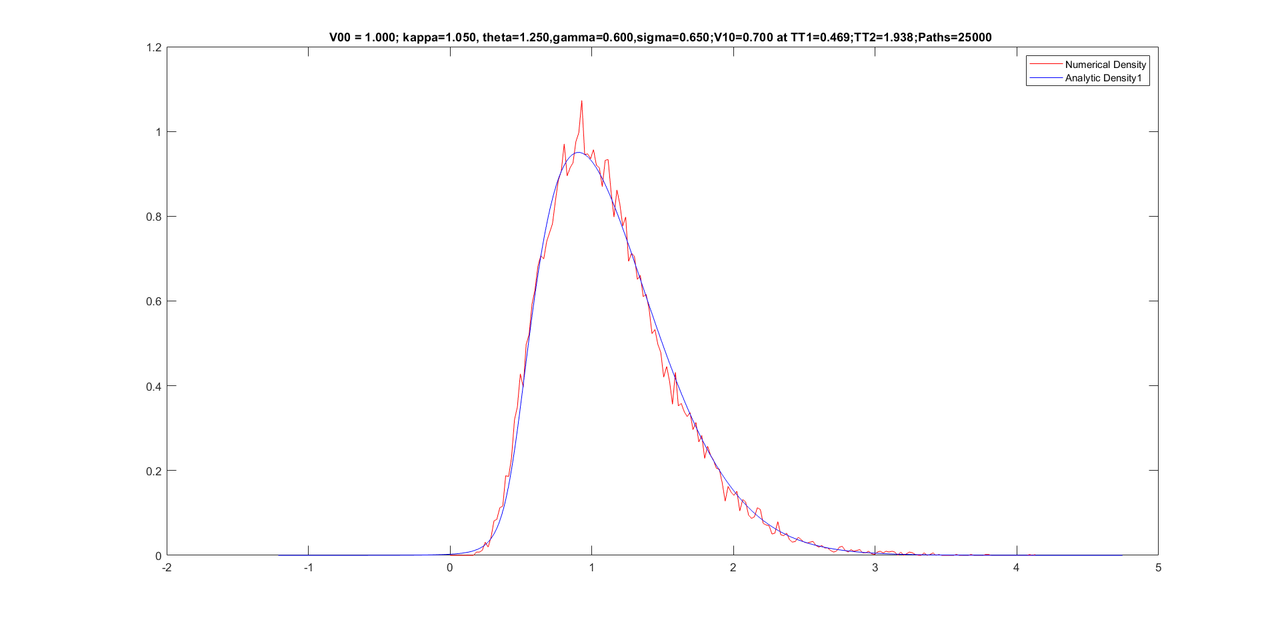
Friends, here are some graphs for various conditional densities. I have corrected for tail of the density at the end of the program by calculating one dimensional moments of the conditional Z-series. Sixth moments is then increased until the tail re-appears. Once the tail is fine, I reconstruct the density from new moments (five old moments + sixth new moment).
However, the above process of increasing sixth moment slightly rotates the density somewhat which is undesirable. I am trying to fix it with some work I did several years ago. I hope that undesirable rotation in the density would end and the density would also have a proper tail once I apply another new method on this.
I will post the matlab program used to make these graphs in a little bit.
Please note that conditional density is \[ P_Y( Y(T_2) \,|\, X(T_1)=V_{10})\,\]
Here are the graphs with parameters on the title of graphs.
.
.
.
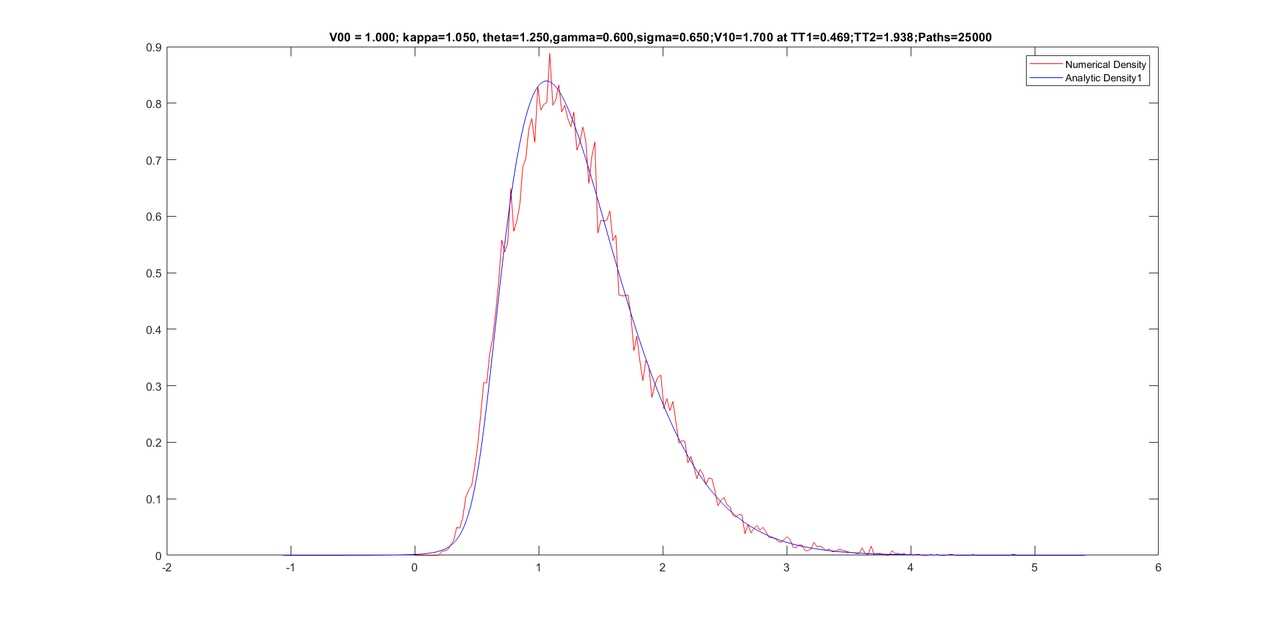
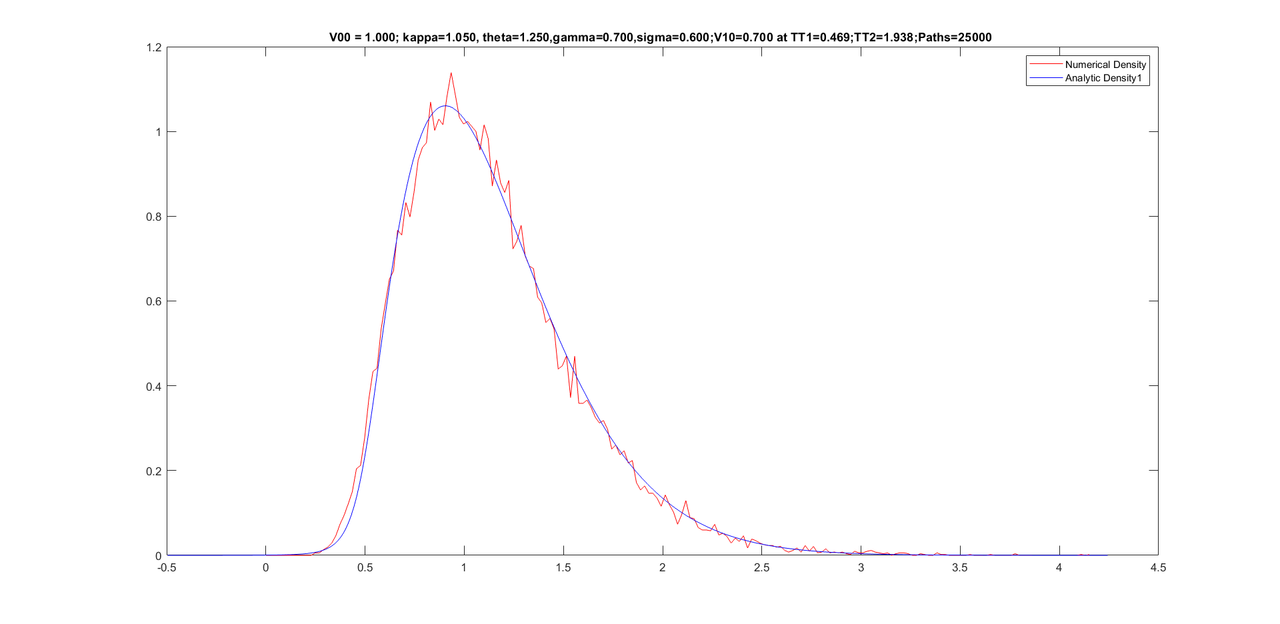
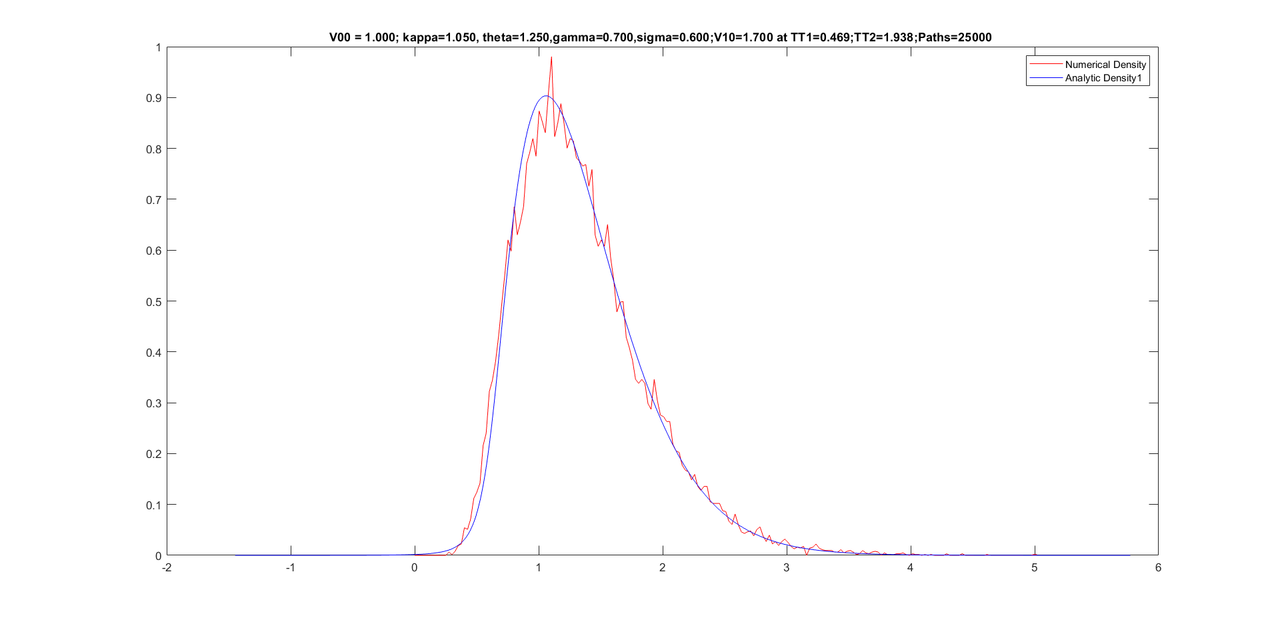
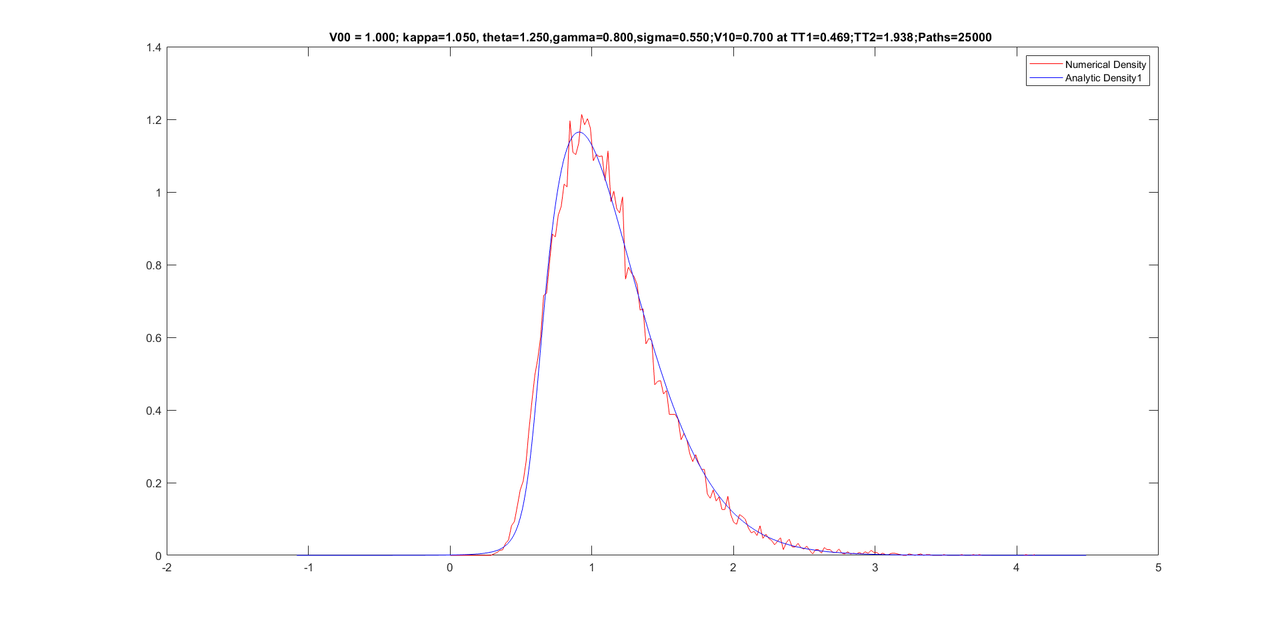
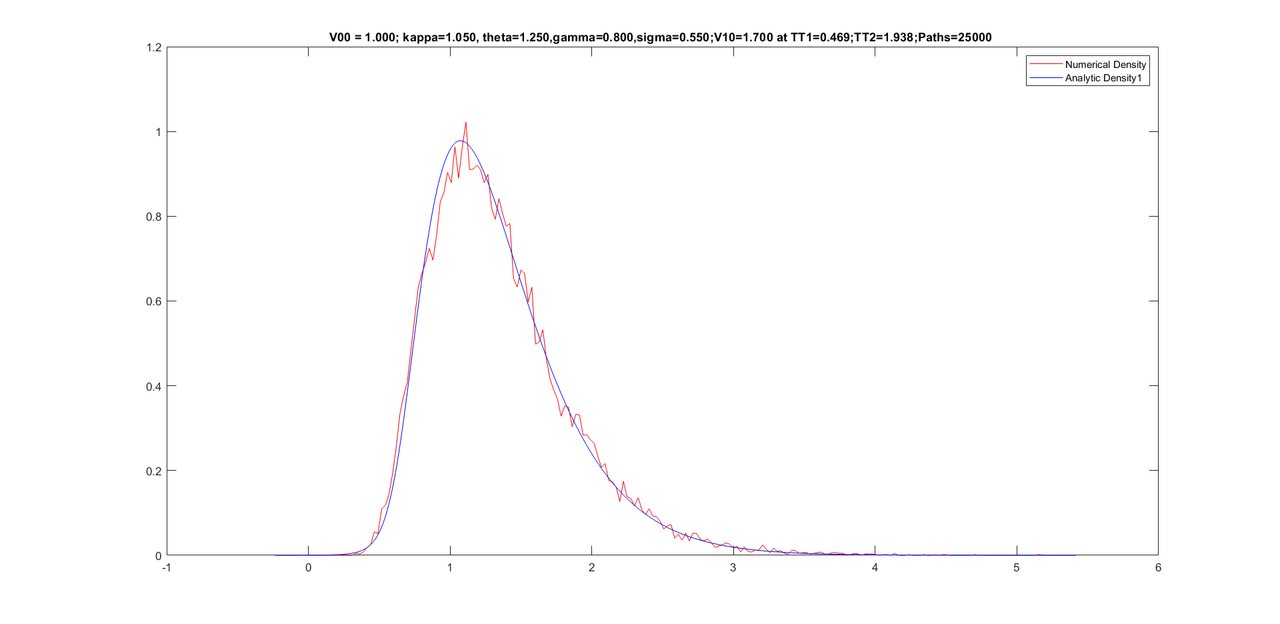
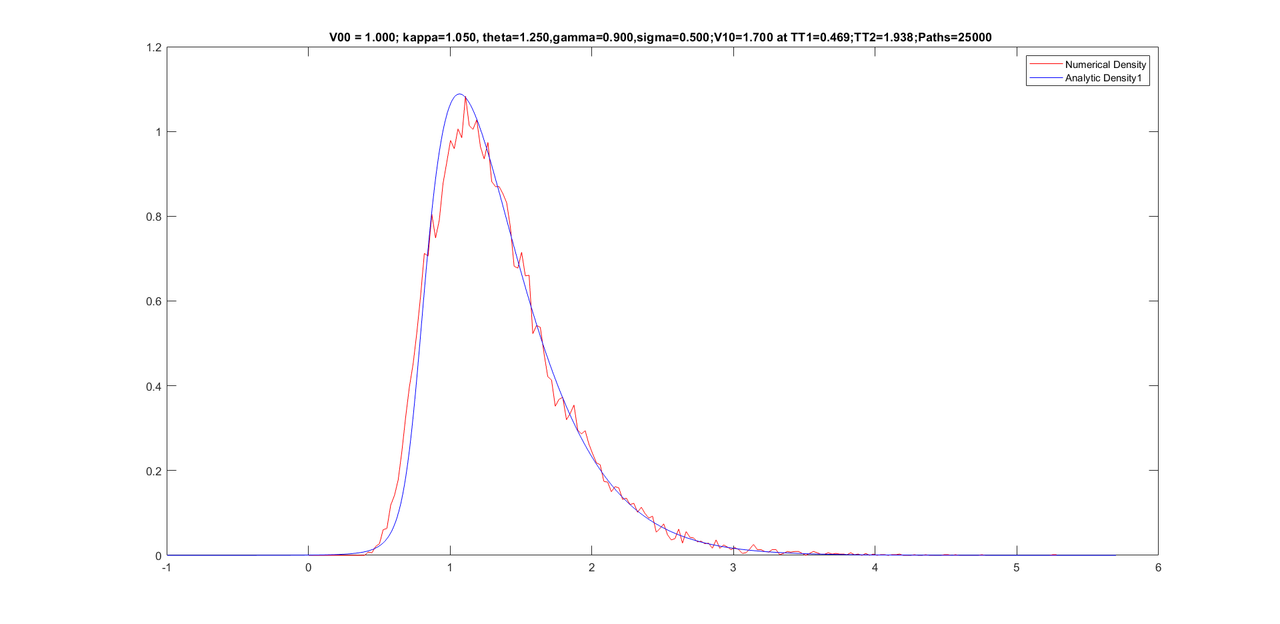
However, the above process of increasing sixth moment slightly rotates the density somewhat which is undesirable. I am trying to fix it with some work I did several years ago. I hope that undesirable rotation in the density would end and the density would also have a proper tail once I apply another new method on this.
I will post the matlab program used to make these graphs in a little bit.
Please note that conditional density is \[ P_Y( Y(T_2) \,|\, X(T_1)=V_{10})\,\]
Here are the graphs with parameters on the title of graphs.
.
.
.










You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
I am posting most of the functions required to run the program. Functions recently posted might not be included unless I changed them. If you cannot find any function, please search for it on the thread using search functionality.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Code: Select all
function []= ConditionalDensityHermitesBivariateNewtonIters02()
%SV SDE is
%dV(t)=mu1 V(t)^beta1 dt+ mu2 V(t)^beta2 dt + sigma0 V(t)^gamma dZ(t)
%In mean reverting SDEs we ususally have
%mu1= kappaV * thetaV
%beta1=0
%mu2=-kappa
%beta2=0
%NDim=4;%Three assets and one SV.
%%%%%%%%%%%%%%%%%%%5
V0=1.00;%.32;
V00=V0;
thetaV=1.250;%.045;%1;%.04;
kappaV=1.05;%1.5;%1.5;
mu1=kappaV*thetaV;
mu2=-kappaV;
beta1=0;
beta2=1;
gamma=.9;%.950;
sigma0=.5%.45;%
dt=.03125/2;
Tt=64*2;
T=Tt*dt;
seed0=52130649;
rng(seed0, 'twister')
paths=25000;
V(1:paths,1)=V0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
TT1=30; %Transition distribution start
TT2=124; %Transition distribution end
Random2(1:paths/2,1)=0;
for tt=1:Tt
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
if(tt==TT1)
Xin(1:paths,1)=V(1:paths,1);
end
if(tt==TT2)
Yin(1:paths,1)=V(1:paths,1);
end
end
str=input("I have reached stone 1");
Order=5;
%The function below does initial analytics of caclulation of 2D conditional
%and joint densities. We want to use the result from this function as a
%Starting guess/seed to Newton derivatives based optimization method.
[YCoeffHH,XYCoeffHH,XCoeffH,Coeffyx,YCoeffH] =CalculateBivariateHermiteSeries01(Yin,Xin,Order);
for qq1=1:Order+1
XMoments(qq1)=sum(Xin(1:paths).^qq1)/paths;
end
[XCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(XCoeffH(1:Order+1),Order);
[XCoeffZ(1),XCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(XMoments,XCoeffZ(2:6));
YCoeffHH(1:Order+1,Order:Order+1)=YCoeffHH(1:Order+1,Order:Order+1)/100000;
YCoeffHH(Order:Order+1,1:Order+1)=YCoeffHH(Order:Order+1,1:Order+1)/100000;
%The above 2D Conditional density calculated from regression is used as an
%input seed to Newton method. YCoeffHH is input as a seed to Newton method
%after converting it to a 2D Z-series.
str=input("I have reached stone 2");
%Below, we calculate Target cross-moments of Y and X from data.
for pp1=1:Order+1
for qq1=1:Order+1
MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Yin(1:paths).^pp1.*Xin(1:paths).^qq1)/paths;
end
end
% for pp1=1:Order+1
% pp4=6;
% pp3=5;
% pp2=4;
% pp1=3;
% if((MomentsYX0((pp4-1)*(Order+1)+qq1,1)/MomentsYX0((pp3-1)*(Order+1)+qq1,1))<(MomentsYX0((pp2-1)*(Order+1)+qq1,1)/MomentsYX0((pp1-1)*(Order+1)+qq1,1)))
% MomentsYX0((pp4-1)*(Order+1)+qq1,1)=MomentsYX0((pp3-1)*(Order+1)+qq1,1)*(MomentsYX0((pp2-1)*(Order+1)+qq1,1)/MomentsYX0((pp1-1)*(Order+1)+qq1,1));
%
% str=input("Moments are being altered")
% end
% %for qq1=1:Order+1
% % MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Yin(1:paths).^pp1.*Xin(1:paths).^qq1)/paths;
% %end
% end
%Before we enter Newton optimization function, we want to convert 2D and 1D hermite
%Series to Z-series.
[XCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(XCoeffH(1:Order+1),Order);
[YCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffH(1:Order+1),Order);
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
OrderY=Order;
OrderX=Order;
[Y1DMoments]=CalculateMomentsOfZSeries(YCoeffZ(1),YCoeffZ(2:6),5,6)
MaxIter0=30;
YCoeffZZ=CalculateSmoothingGuessDensity2D(YCoeffZZ,XCoeffZ,MomentsYX0,Y1DMoments,OrderY,OrderX,MaxIter0)
str=input("Look at smoothing results")
MaxIter=3000;
[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeries(YCoeffZZ,XCoeffZ,Order,MomentsYX0,Y1DMoments,MaxIter);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
% Order=7
% YCoeffHH(1:Order+1,Order:Order+1)=0.0;%YCoeffHH(1:Order+1,Order:Order+1)/100000;
% YCoeffHH(Order:Order+1,1:Order+1)=0.0;%YCoeffHH(Order:Order+1,1:Order+1)/100000;
%
% for pp1=1:Order+1
% for qq1=1:Order+1
% MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Yin(1:paths).^pp1.*Xin(1:paths).^qq1)/paths;
% end
% end
%
%MaxIter0=30;
%YCoeffZZ=CalculateSmoothingGuessDensity2D(YCoeffZZ,XCoeffZ,MomentsYX0,Y1DMoments,OrderY,OrderX,MaxIter0);
%str=input("Look at smoothing results")
%MaxIter=200;
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeries(YCoeffZZ,XCoeffZ,Order,MomentsYX0,Y1DMoments,MaxIter);
%YCoeffZZ is the 2D conditional Z-series of Y given X [Y|X](Zy,Zx)
%that is the result of optimization method and is calibrated to Cross-moments of Y and X.
%MaxIter0=30;
%YCoeffZZ=CalculateSmoothingGuessDensity2D(YCoeffZZ,XCoeffZ,MomentsYX0,Y1DMoments,OrderY,OrderX,MaxIter0);
%str=input("Look at smoothing---3 results")
OrderY=Order;
OrderX=Order;
NMoments=6;
[MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZ,OrderY,OrderX)
%The name of above function is slightly misleading. It calculates mean and
%second moment
[Y1DMoments]=CalculateMomentsOfZSeries(YCoeffZ(1),YCoeffZ(2:6),5,6)
[YMoments] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,OrderY,OrderX,NMoments);
Y1DMoments
YMoments
%Y1DMoments(2)-Y1DMoments(1).^2
%VarZZ
str=input("Look at comparison of second moments/moments");
YCoeffZZ
%AMat
%MomentsYX0
%Below Check the difference between model moments and target moments.
%AMat-MomentsYX0
%Below, we convert the 2D Conditional Z-series of [Y|X](Zy,Zx) into 2D
%Conditional Hermite Seiries of [Y|X](Zy,Zx).
[YCoeffHH] = ConvertZSeriesToHermiteSeries2D(YCoeffZZ,Order+1,Order+1)
% MMul1=sqrt(YCoeffHH(1,1).^2+YCoeffHH(1,2).^2+YCoeffHH(1,3).^2*2+YCoeffHH(1,4).^2*6+YCoeffHH(1,5).^2*24+YCoeffHH(1,6).^2*120)
% YCoeffH(1)
%
% %YCoeffHH(1,:)=YCoeffHH(1,:)*abs(YCoeffH(1))./MMul1;
%
%
% MMul2=sqrt(YCoeffHH(2,1).^2+YCoeffHH(2,2).^2+YCoeffHH(2,3).^2*2+YCoeffHH(2,4).^2*6+YCoeffHH(2,5).^2*24+YCoeffHH(2,6).^2*120)
% YCoeffH(2)
%
% MMul3=sqrt(YCoeffHH(3,1).^2+YCoeffHH(3,2).^2+YCoeffHH(3,3).^2*2+YCoeffHH(3,4).^2*6+YCoeffHH(3,5).^2*24+YCoeffHH(3,6).^2*120)
% YCoeffH(3)
%
%
% MMul4=sqrt(YCoeffHH(4,1).^2+YCoeffHH(4,2).^2+YCoeffHH(4,3).^2*2+YCoeffHH(4,4).^2*6+YCoeffHH(4,5).^2*24+YCoeffHH(4,6).^2*120)
% YCoeffH(4)
%
% MMul5=sqrt(YCoeffHH(5,1).^2+YCoeffHH(5,2).^2+YCoeffHH(5,3).^2*2+YCoeffHH(5,4).^2*6+YCoeffHH(5,5).^2*24+YCoeffHH(5,6).^2*120)
% YCoeffH(5)
%
%
% MMul6=sqrt(YCoeffHH(6,1).^2+YCoeffHH(6,2).^2+YCoeffHH(6,3).^2*2+YCoeffHH(6,4).^2*6+YCoeffHH(6,5).^2*24+YCoeffHH(6,6).^2*120)
% YCoeffH(6)
%
% % YCoeffHH(1,:)=YCoeffHH(1,:)*abs(YCoeffH(1))./MMul1;
% % YCoeffHH(2,:)=YCoeffHH(2,:)*abs(YCoeffH(2))./MMul2;
% % YCoeffHH(3,:)=YCoeffHH(3,:)*abs(YCoeffH(3))./MMul3;
% % YCoeffHH(4,:)=YCoeffHH(4,:)*abs(YCoeffH(4))./MMul4;
% % YCoeffHH(5,:)=YCoeffHH(5,:)*abs(YCoeffH(5))./MMul5;
% % YCoeffHH(6,:)=YCoeffHH(6,:)*abs(YCoeffH(6))./MMul6;
%
%
%
%
str=input("Look at comparison of coefficients")
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%In this block, we do conditional Monte Carlo of SDE which is the true
%numerical 1D conditional density of Y conditional on X having a given
%value. This value of X on which we are conditionin is defined by V10 below.
%We can alter V10 below and it will take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
V10=1.70;
V(1:paths)=V10;
Random2(1:paths,1)=0;
for tt=TT1+1:TT2
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
end
%Below
NoOfBins=200;
MaxCutOff=10;
[XDensity,IndexOut,IndexMax] = MakeDensityFromSimulation_Infiniti_NEW(V,paths,NoOfBins,MaxCutOff );
clf;
plot(IndexOut(1:IndexMax),XDensity(1:IndexMax),'r');
hold on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%Below, we calculate the value of Zx0 corresponding to X0 (here V10). This
%comes from inverting the Z-series of X so that X=V10;
xOrder=Order;
yOrder=Order;
[Zx0] = CalculateZgivenXAndHSeriesCoeffs(V10,XCoeffH,xOrder);
%Below, we collapse two dimensional pdf of Y|X to one dimensional pdf given
%Zx i.e. this Y|X=X(Zx)
%Here we take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
He(1)=1;
He(2)=Zx0;
He(3)=Zx0^2-1;
He(4)=Zx0^3-3*Zx0;
He(5)=Zx0^4-6*Zx0.^2+3;
He(6)=Zx0^5-10*Zx0.^3+15*Zx0;
He(7)=Zx0^6-15*Zx0.^4+45*Zx0.^2-15;
He(8)=Zx0^7-21*Zx0.^5+105*Zx0.^3-105*Zx0;
YCoeffh(1:Order+1)=0;
for hh=1:yOrder+1
for hh2=1:xOrder+1
YCoeffh(hh)=YCoeffh(hh)+YCoeffHH(hh,hh2).*He(hh2);
end
end
[YCoeffz(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffh(1:Order+1),Order);
%
%
% %[IsValidFlag] = CheckIsValidDensityPN(YCoeffz(1),YCoeffz(2:Order+1));
% [PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(YCoeffz(1),YCoeffz(2:Order+1));
% PIsValidFlag
% NIsValidFlag
%
%
% for mm=1:100
% [PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(YCoeffz(1),YCoeffz(2:Order+1));
% if((NIsValidFlag==0)&&(PIsValidFlag==1))
% YCoeffz(5)=YCoeffz(5)-.01*abs(YCoeffz(5));
% YCoeffz(6)=YCoeffz(6)+.001*abs(YCoeffz(6));
% %YCoeffz(3)=YCoeffz(3)-.001*abs(YCoeffz(3));
% end
%
% if((PIsValidFlag==0)&&(NIsValidFlag==1))
% YCoeffz(5)=YCoeffz(5)+.01*abs(YCoeffz(5));
% YCoeffz(6)=YCoeffz(6)+.001*abs(YCoeffz(6));
% %YCoeffz(3)=YCoeffz(3)-.001*abs(YCoeffz(3));
% end
%
% if((NIsValidFlag==0)&&(PIsValidFlag==0))
% YCoeffz(6)=YCoeffz(6)+.01*abs(YCoeffz(6));
% %YCoeffz(3)=YCoeffz(3)-.001*abs(YCoeffz(3));
% end
%
% end
%
% [YCoeffh] = ConvertZSeriesToHermiteSeriesNew(YCoeffz,Order)
%
PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh(2:yOrder+1),'b')
%hold on
%PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh1(2:yOrder+1),'g')
title(sprintf('V00 = %.3f; kappa=%.3f, theta=%.3f,gamma=%.3f,sigma=%.3f;V10=%.3f at TT1=%.3f;TT2=%.3f;Paths=%d ',V00, kappaV, thetaV,gamma,sigma0, V10,(TT1*dt),(TT2*dt),paths));%,sprintf('theta= %f', theta), sprintf('kappa = %f', kappa),sprintf('sigma = %f', sigma0),sprintf('T = %f', T));
legend({'Numerical Density','Analytic Density1'}, ...
'Location','northeast')
str=input("This is the first version without altering the moments of conditional density")
% %[IsValidFlag] = CheckIsValidDensityPN(YCoeffz(1),YCoeffz(2:Order+1));
[PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(YCoeffz(1),YCoeffz(2:Order+1));
PIsValidFlag
NIsValidFlag
LoopIter=0;
Mul6(1)=.66;
Mul6(2)=.8;
Mul6(3)=.9;
Mul6(4)=1.0;
Mul6(5)=1.1;
while(((PIsValidFlag==0)||(NIsValidFlag==0))&&(LoopIter<5))
LoopIter=LoopIter+1;
YCoeffh
Y2Coeffz=YCoeffz;
Mean=Y2Coeffz(1)+(Y2Coeffz(3)+3*Y2Coeffz(5));
Y2Coeffz(1)=-(Y2Coeffz(3)+3*Y2Coeffz(5));
[YMoments]=CalculateMomentsOfZSeries(Y2Coeffz(1),Y2Coeffz(2:6),5,6)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
abs(YMoments(3:6))./abs(YMoments(2:5))
YMoments(2:6)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%555
if(abs(YMoments(6)/YMoments(5))<abs(YMoments(4)/YMoments(3))*Mul6(LoopIter))
YMoments(6)=abs(YMoments(5).*YMoments(4)./YMoments(3)*Mul6(LoopIter))
end
[Y3Coeffz(1),Y3Coeffz(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YMoments,Y2Coeffz(2:6));
Y3Coeffz(1)=Mean-(Y2Coeffz(3)+3*Y2Coeffz(5));
[PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(Y3Coeffz(1),Y3Coeffz(2:Order+1));
PIsValidFlag
NIsValidFlag
end
if(LoopIter==0)
Y3Coeffz=YCoeffz;
end
clf;
plot(IndexOut(1:IndexMax),XDensity(1:IndexMax),'r');
hold on
PlotZSeriesDensity(Y3Coeffz(1),Y3Coeffz(2:yOrder+1),'b')
title(sprintf('V00 = %.3f; kappa=%.3f, theta=%.3f,gamma=%.3f,sigma=%.3f;V10=%.3f at TT1=%.3f;TT2=%.3f;Paths=%d ',V00, kappaV, thetaV,gamma,sigma0, V10,(TT1*dt),(TT2*dt),paths));%,sprintf('theta= %f', theta), sprintf('kappa = %f', kappa),sprintf('sigma = %f', sigma0),sprintf('T = %f', T));
legend({'Numerical Density','Analytic Density1'}, ...
'Location','northeast')
str=input("This is the Second version after possibly altering the moments of conditional density when needed")
end.
.
.
Code: Select all
function [YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeries(YCoeffZZ,XCoeffZ,Order,MomentsYX0,MomentsY,MaxIter)
%YCoeffZZ is 2D Z-series conditional on X denoted in literature as [Y|X](Zy,Zx)
%The way to construct Z-series from YCoeffZZ is sum of terms YCoeffZZ(n,m) Zy^{n-1)Zx^{m-1}.
%YCoeffZZ(1:Order+1,1:Order+1) is a 2D array containing coefficients of 2D
%Z-Series of Conditional distribution of Y given X (or Z_x).
%XCoeffZ(1:Order+1) is a one dimensional Z-series of X. The way to construct the Z-series is
%sum of terms XCoeffZ(m) Zx^{m-1}. It has dimensiona YCoeffZ(1:Order+1).
% The way to calculate the cross-product/cross-moments: 2D product of Z-series
% ([Y|X](Zy,Zx))^(pp1-1) *(X(Zx))^qq2/E[([Y|X](Zy,Zx))^(pp1-1)*(X(Zx))^qq2]
%MomentsYX0 is a 1D array containing all the target cross-moments ((Order+1)*(Order+1))stacked in an array.
%%AMat gives us all the expected model cross-moments ((Order+1)*(Order+1))stacked in an array.
%DMat contains Jacobian that calculates ((Order+1)*(Order+1)) derivatives
%for each cross-moment hence its size is ((Order+1)*(Order+1)) *,((Order+1)*(Order+1))
%Below, we calculate AMat and DMat.
[AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
%CalculateMomentsAndDerivativesFor2DNewton_0_BumpCheck
mul=.00625*4;
mulCount=0;
mulCount0=0;
%Below is initial value of Objective function calculated from input array
%target and model sum of squared differences of cross-moments.
ObjMax=sum((AMat-MomentsYX0).^2);
FailCount=0;
%Iterations=MaxIter;
Mul_Gauss=1;
iter=0;
while((sum((AMat-MomentsYX0).^2)>.001)&&(iter<MaxIter))
iter=iter+1;
%Below we stack all coefficients of YCoeffZZ to be optimized in a
%single Newton work-horse array da.
for pp2=1:Order+1
for qq2=1:Order+1
da((pp2-1)*(Order+1)+qq2,1)=YCoeffZZ(pp2,qq2);
end
end
for pp2=1:Order+1
for qq2=1:Order+1
F((pp2-1)*(Order+1)+qq2,1)=(AMat((pp2-1)*(Order+1)+qq2,1)-MomentsYX0((pp2-1)*(Order+1)+qq2,1));
end
end
%DMat0 is matrix with diagonal weights that have to be applied to Jacobian matrix in order to turn
%the Newton method closer to Steepest descent.
for pp1=1:Order+1
for qq1=1:Order+1
for pp2=1:Order+1
for qq2=1:Order+1
if((pp1-1)*(Order+1)+qq1==(pp2-1)*(Order+1)+qq2)
DMat0((pp1-1)*(Order+1)+qq1,(pp2-1)*(Order+1)+qq2)=Mul_Gauss*.0001;
end
end
end
end
end
%mul and mul_Gauss are two different multipliers that work in the algorithm.
da=da-mul*((DMat0+DMat)\F);
%Assign the new Newton values of Coefficients from Newton work-horse
%array to a temporary array YCoeffZZnew. If the objective function with
%this new array increases, we will declare the iteration a success and
%assign this YCoeffZZnew to original array YCoeffZZ.
for pp2=1:Order+1
for qq2=1:Order+1
YCoeffZZnew(pp2,qq2)=da((pp2-1)*(Order+1)+qq2,1);
end
end
if(rem(iter,10)==0)
[MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZnew,Order,Order);
YCoeffZZnew=YCoeffZZnew*sqrt(MomentsY(2))./sqrt(VarZZ);
[MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZnew,Order,Order);
YCoeffZZnew(1,1)=YCoeffZZnew(1,1)+MomentsY(1)-MeanZZ;
end
if(rem(iter,50)==0)
MaxIter0=1;
[YCoeffZZnew] = CalculateSmoothingGuessDensity2D(YCoeffZZnew,XCoeffZ,MomentsYX0,MomentsY,Order,Order,MaxIter0);
end
%Calculate model cross-moments with new values to find the objective
%function to decide whether to accept the iteration value of reject it.
[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
ObjNew=sum((AMat-MomentsYX0).^2);
ObjNew
ObjMax
iter
%str=input("Look at values");
MulGaussHigh=10^8;
MulGaussLow=1;
if(Mul_Gauss>MulGaussHigh)
Mul_Gauss=MulGaussLow;
end
if(ObjNew<ObjMax)
%If objective function decreases assign YCoeffZZnew to YCoeffZZ
ObjMax=ObjNew;
YCoeffZZ=YCoeffZZnew;
mulCount0=mulCount0+1;
if(mulCount0>=4)
Mul_Gauss=Mul_Gauss*.75;
if(Mul_Gauss<1)
Mul_Gauss=1;
end
mulCount0=0;
end
mul=mul*2; %On success increase the step size.
if(mul>1)
mul=1;
end
FailCount=0;
else
mul=mul*.5; %On failure, decrease the step size.
if(mul<.00625/8)
mul=.00625*2;
mulCount=mulCount+1;
end
if(mulCount>=4)
Mul_Gauss=Mul_Gauss*1.5;
mul_Count=0;
end
FailCount=FailCount+1;
end
%Calculate model cross-moments and Jacobian derivatives for Next Newton
%type iteration.
[AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
end
% YCoeffZZ
% AMat
% MomentsYX0
% AMat-MomentsYX0
end.
.
.
Code: Select all
function [YCoeffZZBest] = CalculateSmoothingGuessDensity2D(YCoeffZZ,XCoeffZ,MomentsYX0,MomentsY,OrderY,OrderX,MaxIter)
Order=OrderY;
%[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZ,XCoeffZ,OrderY,OrderX)
Iterations=40;
Iterations2=2;
YCoeffZZBest=YCoeffZZ;
[AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
ObjMax=sum((AMat-MomentsYX0).^2);
for iter=1:MaxIter
for pp1=1:Order+1
for qq1=1:Order+1
for iter2=1:Iterations2
[AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
DiffMoment=AMat((pp1-1)*(Order+1)+qq1)-MomentsYX0((pp1-1)*(Order+1)+qq1);
DDiff=DMat((pp1-1)*(Order+1)+qq1,(pp1-1)*(Order+1)+qq1);
%YCoeffZZ=YCoeffZZ;
YCoeffZZ(pp1,qq1)=YCoeffZZ(pp1,qq1)-DiffMoment/DDiff;
end
[MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZ,Order,Order);
YCoeffZZ=YCoeffZZ*sqrt(MomentsY(2))./sqrt(VarZZ);
[MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZ,Order,Order);
YCoeffZZ(1,1)=YCoeffZZ(1,1)+MomentsY(1)-MeanZZ;
[AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
ObjNew=sum((AMat-MomentsYX0).^2);
if(ObjNew<ObjMax)
%If objective function decreases assign YCoeffZZnew to YCoeffZZ
ObjMax=ObjNew;
YCoeffZZBest=YCoeffZZ;
end
end
end
[AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
ObjNew=sum((AMat-MomentsYX0).^2);
if(ObjNew<ObjMax)
%If objective function decreases assign YCoeffZZnew to YCoeffZZ
ObjMax=ObjNew;
YCoeffZZBest=YCoeffZZ;
end
if(ObjNew>2*ObjMax)
% YCoeffZZ=YCoeffZZBest;
end
ObjNew
ObjMax
iter
end
end
% for iter=1:Iterations
%
% for pp1=1:Order+1
% for qq1=1:Order+1
%
% for iter2=1:Iterations2
% [AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
%
% DiffMoment=AMat((pp1-1)*(Order+1)+qq1)-MomentsYX0((pp1-1)*(Order+1)+qq1);
% DDiff=DMat((pp1-1)*(Order+1)+qq1,(pp1-1)*(Order+1)+qq1);
% YCoeffZZnew=YCoeffZZ;
% YCoeffZZnew(pp1,qq1)=YCoeffZZ(pp1,qq1)-DiffMoment/DDiff;
% end
%
% [MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZnew,Order,Order);
% YCoeffZZnew=YCoeffZZnew*sqrt(MomentsY(2))./sqrt(VarZZ);
% [MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZnew,Order,Order);
% YCoeffZZnew(1,1)=YCoeffZZnew(1,1)+MomentsY(1)-MeanZZ;
% [AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZnew,XCoeffZ,Order);
% ObjNew=sum((AMat-MomentsYX0).^2);
% if(ObjNew<ObjMax)
% %If objective function decreases assign YCoeffZZnew to YCoeffZZ
% ObjMax=ObjNew;
% YCoeffZZ=YCoeffZZnew;
% end
% end
%
% end
% [AMat,DMat] = CalculateMomentsAndDerivativesFor2DNewton_0(YCoeffZZ,XCoeffZ,Order);
% ObjNew=sum((AMat-MomentsYX0).^2);
% if(ObjNew<ObjMax)
% %If objective function decreases assign YCoeffZZnew to YCoeffZZ
% ObjMax=ObjNew;
% YCoeffZZBest=YCoeffZZ;
% end
%
% ObjNew
% ObjMax
% iter
%
%
% end.
.
.
Code: Select all
function [PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(cc0,cc)
%Roughly checks if the density is valid. It is not a definitive check but
%just a rough one but mostly works.
if(cc(1)>0)
Z(1)=2.0;
Z(2)=3.0;
Z(3)=3.9;
Z(4)=4.2;
Z(5)=-2.3;
Z(6)=-2.7;
Z(7)=-3.3;
Z(8)=-3.9;
Z(9)=-4.3;
if(length(cc)==7)
X=cc0 + cc(1) * Z+ cc(2) * Z.^2+ cc(3) * Z.^3+ cc(4) * Z.^4+ cc(5) * Z.^5+ cc(6) * Z.^6+ cc(7) * Z.^7;
end
if(length(cc)==5)
X=cc0 + cc(1) * Z+ cc(2) * Z.^2+ cc(3) * Z.^3+ cc(4) * Z.^4+ cc(5) * Z.^5;
end
PIsValidFlag=0;
if ((X(4)>=X(3)) && (X(3)>X(2)) && (X(2)>X(1))&&(X(1)>X(5)) )
PIsValidFlag=1;
end
NIsValidFlag=0;
if ((X(5)>X(6))&&(X(6)>X(7)) && (X(7)>X(8))&& (X(8)>X(9)))
NIsValidFlag=1;
end
else
Z(1)=2.0;
Z(2)=3.0;
Z(3)=3.9;
Z(4)=4.2;
Z(5)=-2.3;
Z(6)=-2.7;
Z(7)=-3.3;
Z(8)=-3.9;
Z(9)=-4.3;
if(length(cc)==7)
X=cc0 + cc(1) * Z+ cc(2) * Z.^2+ cc(3) * Z.^3+ cc(4) * Z.^4+ cc(5) * Z.^5+ cc(6) * Z.^6+ cc(7) * Z.^7;
end
if(length(cc)==5)
X=cc0 + cc(1) * Z+ cc(2) * Z.^2+ cc(3) * Z.^3+ cc(4) * Z.^4+ cc(5) * Z.^5;
end
PIsValidFlag=0;
if ((X(4)>=X(3)) && (X(3)>X(2)) && (X(2)>X(1))&&(X(1)>X(5)) )
PIsValidFlag=1;
end
NIsValidFlag=0;
if ((X(5)>X(6))&&(X(6)>X(7)) && (X(7)>X(8))&& (X(8)>X(9)))
NIsValidFlag=1;
end
end
end
.
.
.
Code: Select all
function [c0,c] = CalculateZSeriesDensityFromRawMomentsM6(rMu,bGuess)
mOrder=6;
[Mu1,cMu] = ConvertRawMomentsToCentralMoments(rMu,mOrder);
sMu(1)=0;
sMu(2)=1;
sMu(3)=cMu(3)/cMu(2).^1.5;
sMu(4)=cMu(4)/cMu(2).^2.0;
sMu(5)=cMu(5)/cMu(2).^2.5;
sMu(6)=cMu(6)/cMu(2).^3.0;
%sMu(7)=cMu(7)/cMu(2).^3.5;
%sMu(8)=cMu(8)/cMu(2).^4.0;
w(mOrder)=1;
for nn=mOrder-1:-1:1
w(nn)=w(nn+1).*(nn+1)*(nn);
end
%w(2)=w(2)*1024;
%w(8)=w(8)*2;
%w(10)=w(10)*sqrt(2);
iter=2000;
%bGuess(1:5)=0;
%bGuess(1)=1;
[c0,c] = PreSmoothingGuessAdvancedFromGuessBestNewC5(sMu,bGuess,iter);
SeriesOrder=5;
NMoments=6;
[F,dF] = CalculateMomentsAndDerivatives_0(sMu,c0,c,SeriesOrder,SeriesOrder,NMoments);
da(1,1)=c0;
da(2:SeriesOrder+1,1)=c(1:SeriesOrder);
[Moments] = CalculateMomentsOfZSeries(c0,c,SeriesOrder,NMoments);
Moments
sMu
%str=input('Look at comparison of moments');
%Replace with your own more intelligent objective function if you like.
%ObjBest=100000*(abs(sMu(1)-Moments(1)))+abs(sMu(2)-Moments(2))+abs((sMu(3)-Moments(3))^(1/1.5))+abs((sMu(4)-Moments(4))^(1/2.0)) + ...
% abs((sMu(5)-Moments(5))^(1/2.0))+abs((sMu(6)-Moments(6))^(1/2.0));
[ObjBest] = CalculateObjMoment(sMu,Moments,w,mOrder)
b0Best=c0;
bBest(1:SeriesOrder)=c(1:SeriesOrder);
nn=0;
while((nn<1000)&&((abs(F(1,1))>.000000000001) || (abs(F(2,1))>.000000000001) || (abs(F(3,1))>.000000000001) || (abs(F(4,1))>.00000000001)|| (abs(F(5,1))>.00000000001)|| (abs(F(6,1))>.00000000001) ))
nn=nn+1;
%Below Newton matrix equation to improve the Z-series coefficients guess at previous step.
if(nn<10)
da=da-10*dF\F;
elseif(nn<20)
da=da-5*dF\F;
elseif(nn<40)
da=da-2*dF\F;
else
da=da-dF\F;
end
%b0=median
b0=da(1,1);
b(1:SeriesOrder)=da(2:SeriesOrder+1,1);
%[F,dF] = CalculateCumulantsAndDerivativesFromMoments_0(C,b0,b,SeriesOrder,SeriesOrder,NoOfCumulants);
[F,dF] = CalculateMomentsAndDerivatives_0(sMu,b0,b,SeriesOrder,SeriesOrder,NMoments);
[IsValidFlag] =1;% CheckIsValidDensity(b0,b);
[Moments] = CalculateMomentsOfZSeries(b0,b,SeriesOrder,NMoments);
[ObjNew] = CalculateObjMoment(sMu,Moments,w,mOrder)
%ObjNew=100000*(abs(sMu(1)-Moments(1)))+abs(sMu(2)-Moments(2))+abs((sMu(3)-Moments(3))^(1/1.5))+abs((sMu(4)-Moments(4))^(1/2.0)) + ...
%abs((sMu(5)-Moments(5))^(1/2.0))+abs((sMu(6)-Moments(6))^(1/2.0));
if((ObjBest>ObjNew) &&( IsValidFlag))
ObjBest=ObjNew;
b0Best=b0;
bBest(1:SeriesOrder)=b(1:SeriesOrder);
end
da(1,1)=b0;
da(2:SeriesOrder+1,1)=b(1:SeriesOrder);
end
c0=b0Best;%Best;
c(1:SeriesOrder)=bBest;%Best(1:SeriesOrder);
[Moments] = CalculateMomentsOfZSeries(c0,c,SeriesOrder,NMoments);
b0Best
bBest
Moments
sMu
cMu(2)
%str=input('Look at fit of density----0000 ')
c0=c0*sqrt(cMu(2));
c=c*sqrt(cMu(2));
c0=c0+Mu1;
end
.
.
Code: Select all
function [c0,c] = PreSmoothingGuessAdvancedFromGuessBestNewC5(cmu,cin,iter)
%Mul=1.0;
SeriesOrder=5;
NMoments=6;
EZ(1)=0;
EZ(2)=1;
for nn=3:NMoments*SeriesOrder+SeriesOrder+2
if rem(nn,2)==1
EZ(nn)=0;
else
EZ(nn)=EZ(nn-2)*(nn-1);
EZ(nn);
end
end
c0=-(cin(2)+3*cin(4)); %This is for zero mean condition.
c=cin;
MaxIter=100;
for nn=1:iter %increase the iterations over coefficients if neeeded
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
tolerance=.0000001*cmu(3);
mm=0;
while ((abs(M3-cmu(3)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(2)=c(2)-(M3-cmu(3))/dc2;
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[c0,c] = IterateSmoothingGuessOverPreviousMomentsC5(cmu,c,3,2,EZ);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
tolerance=.0000001*cmu(4);
mm=0;
while ((abs(M4-cmu(4)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(3)=c(3)-(M4-cmu(4))/dc3;
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
end
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[c0,c] = IterateSmoothingGuessOverPreviousMomentsC5(cmu,c,4,2,EZ);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[M5,dc4] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,5,EZ);
tolerance=.0000001*cmu(5);
mm=0;
while ((abs(M5-cmu(5)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(4)=c(4)-(M5-cmu(5))/dc4;
[M5,dc4] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,5,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[c0,c] = IterateSmoothingGuessOverPreviousMomentsC5(cmu,c,5,2,EZ);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[M6,dc5] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,6,EZ);
tolerance=.0000001*cmu(6);
mm=0;
while ((abs(M6-cmu(6)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(5)=c(5)-(M6-cmu(6))/dc5;
[M6,dc5] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,6,EZ);
end
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[c0,c] = IterateSmoothingGuessOverPreviousMomentsC5(cmu,c,6,2,EZ);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
end
end
.
.
.
Code: Select all
function [EnMoment,dEnMomentdCoeff] = CalculateParticularMomentAndDerivativeOfItsCoeff(a0,a,SeriesOrder,nMoment,EZ)
% if(SeriesOrder>=8)
% a0=-(a(2)+3*a(4)+15*a(6)+105*a(8));% ---1
% end
% if(SeriesOrder<8)
% a0=-(a(2)+3*a(4)+15*a(6));% ---1
% end
%
% EZ(1)=0;
% EZ(2)=1;
% for nn=3:NMoments*SeriesOrder+NZterms+2
% if rem(nn,2)==1
% EZ(nn)=0;
% else
% EZ(nn)=EZ(nn-2)*(nn-1);
% EZ(nn);
% end
% end
% EZ;
%EXZ(1,1)=1;
%for pp1=1:NZterms
% EXZ(1,pp1+1)=EZ(pp1);
%end
a(SeriesOrder+1:nMoment*SeriesOrder+1+SeriesOrder)=0;
b0=a0;
b=a;
for mm=2:nMoment
[b0,b] =SeriesProduct(a0,a,b0,b,SeriesOrder*mm+SeriesOrder+1);
b(SeriesOrder*mm+1:nMoment*SeriesOrder+SeriesOrder+1)=0;
if(mm==nMoment-1)
dEnMomentdCoeff=b0.*EZ(nMoment-1);
for pp2=1:SeriesOrder*nMoment-1
dEnMomentdCoeff=dEnMomentdCoeff+b(pp2).*EZ(pp2+nMoment-1);
end
dEnMomentdCoeff=dEnMomentdCoeff*nMoment;
end
if(mm==nMoment)
EnMoment=b0;
for pp2=1:SeriesOrder*nMoment
EnMoment=EnMoment+b(pp2).*EZ(pp2);
end
end
end
end
.
.
Code: Select all
function [c0,c] = IterateSmoothingGuessOverPreviousMomentsC5(cmu,c,nMoment,iter,EZ)
MaxIter=7;
SeriesOrder=5;
c0=-(c(2)+3*c(4));
if(nMoment==3)
for nn=1:iter %increase the iterations over coefficients if neeeded
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
tolerance=.0000001*cmu(3);
mm=0;
while ((abs(M3-cmu(3)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(2)=c(2)-(M3-cmu(3))/dc2;
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
if(nMoment==4)
for nn=1:iter %increase the iterations over coefficients if neeeded
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
tolerance=.0000001*cmu(3);
mm=0;
while ((abs(M3-cmu(3)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(2)=c(2)-(M3-cmu(3))/dc2;
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
tolerance=.0000001*cmu(4);
mm=0;
while ((abs(M4-cmu(4)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(3)=c(3)-(M4-cmu(4))/dc3;
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
end
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if(nMoment==5)
for nn=1:iter %increase the iterations over coefficients if neeeded
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
tolerance=.0000001*cmu(3);
mm=0;
while ((abs(M3-cmu(3)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(2)=c(2)-(M3-cmu(3))/dc2;
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
tolerance=.0000001*cmu(4);
mm=0;
while ((abs(M4-cmu(4)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(3)=c(3)-(M4-cmu(4))/dc3;
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
end
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[M5,dc4] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,5,EZ);
tolerance=.0000001*cmu(5);
mm=0;
while ((abs(M5-cmu(5)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(4)=c(4)-(M5-cmu(5))/dc4;
[M5,dc4] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,5,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if(nMoment==6)
for nn=1:iter %increase the iterations over coefficients if neeeded
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
tolerance=.0000001*cmu(5);
mm=0;
while ((abs(M3-cmu(3)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(2)=c(2)-(M3-cmu(3))/dc2;
[M3,dc2] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,3,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
tolerance=.0000001*cmu(5);
mm=0;
while ((abs(M4-cmu(4)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(3)=c(3)-(M4-cmu(4))/dc3;
[M4,dc3] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,4,EZ);
end
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[M5,dc4] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,5,EZ);
tolerance=.0000001*cmu(5);
mm=0;
while ((abs(M5-cmu(5)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(4)=c(4)-(M5-cmu(5))/dc4;
[M5,dc4] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,5,EZ);
end
c0=-(c(2)+3*c(4));
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[M6,dc5] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,6,EZ);
tolerance=.0000001*cmu(6);
mm=0;
while ((abs(M6-cmu(6)) >tolerance ) && (mm<MaxIter))
mm=mm+1;
c(5)=c(5)-(M6-cmu(6))/dc5;
[M6,dc5] = CalculateParticularMomentAndDerivativeOfItsCoeff(c0,c,SeriesOrder,6,EZ);
end
[SecondMoment] = CalculateSecondMomentC5(c0,c);
c=c/sqrt(SecondMoment);
c0=c0/sqrt(SecondMoment);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
end
end
end
.
.
.
Code: Select all
function [SecondMoment] = CalculateSecondMomentC5(a0,a)
SecondMoment=a0^2+a(1)^2 +2* a0* a(2) +3*(a(2).^2+2* a(1).* a(3) +2* a0* a(4))+ ...
15*(a(3).^2 +2 *a(2).* a(4) +2 *a(1).* a(5))+105*(a(4).^2 +2* a(3).* a(5) )+ ...
945*(a(5).^2 );
%a0^2+a1^2+2 a0 a2+3 (a2^2+2 a1 a3+2 a0 a4)+945 a5^2+15 (a3^2+2 a2 a4+2 a1 a5)+105 (a4^2+2 a3 a5)
end
.
.
.
Code: Select all
function [Moments] = CalculateMomentsOfZSeries(a0,a,SeriesOrder,NMoments)
%aa0=a0;
%a0=0;% ---1
EZ(1)=0;
EZ(2)=1;
%LogEZ(2)=0;
for nn=3:NMoments*SeriesOrder
if rem(nn,2)==1
EZ(nn)=0;
else
EZ(nn)=EZ(nn-2)*(nn-1);
%LogEZ(nn)=log(EZ(nn-2))+log(nn-1);
%EZ(nn);
end
end
%EZ
%EZ(1:30)
%str=input('Look at numbers')
a(SeriesOrder+1:SeriesOrder*NMoments+1)=0;
b0=a0;
b=a;
for mm=1:NMoments
if(mm>1)
%[b0,b] =SeriesProductLogarithmic(a0,a,b0,b,SeriesOrder*mm);
[b0,b] =SeriesProduct(a0,a,b0,b,SeriesOrder*mm);
%b0-bb0
%b-bb
%str=input('Look at two products')
b(SeriesOrder*mm+1:SeriesOrder*NMoments+1)=0;
end
% Logb=log(abs(b));
% Signb=sign(b);
EXZ(mm,1)=b0;
for pp2=1:SeriesOrder*mm
if rem(pp2,2)==0
%EXZ(mm,1)=EXZ(mm,1)+exp(Logb(pp2)+LogEZ(pp2)).*Signb(pp2);
EXZ(mm,1)=EXZ(mm,1)+b(pp2).*EZ(pp2);
% b(pp2).*EZ(pp2)
% exp(Logb(pp2)+LogEZ(pp2)).*Signb(pp2)
% mm
% pp2
%str=input('Look at moment values')
end
end
end
for nn=1:NMoments
Moments(nn)=EXZ(nn,1);
end
end
.
.
Code: Select all
function [F,dF] = CalculateMomentsAndDerivatives_0(Ms,a0,a,SeriesOrder,NZterms,NMoments)
%[F,dF] = CalculateCumulantsAndDerivativesFromMoments(C,a0,a,SeriesOrder,SeriesOrder,NoOfCumulants);
%a(1)=a1;
%a(2)=a2;
%a(3)=a3;
%a(4)=a4;
%a(5)=a5;
%a(6)=a6;
%a(7)=a7;
%aa0=a0;
if(NMoments>8)
a0=-(a(2)+3*a(4)+15*a(6)+105*a(8));% ---1
end
if((NMoments==7)||(NMoments==8))
a0=-(a(2)+3*a(4)+15*a(6));% ---1
end
% if(NMoments==6)
% a0=-(a(2)+3*a(4));% ---1
% end
if((NMoments==6)||(NMoments==7))
a0=-(a(2)+3*a(4));% ---1
end
if((NMoments==3)||(NMoments==4))
a0=-(a(2));% ---1
end
EZ(1)=0;
EZ(2)=1;
for nn=3:NMoments*SeriesOrder+NZterms+2
if rem(nn,2)==1
EZ(nn)=0;
else
EZ(nn)=EZ(nn-2)*(nn-1);
EZ(nn);
end
end
EZ;
EXZ(1,1)=1;
for pp1=1:NZterms
EXZ(1,pp1+1)=EZ(pp1);
end
a(SeriesOrder+1:NMoments*SeriesOrder+1)=0;
b0=a0;
b=a;
for mm=1:NMoments
if(mm>1)
[b0,b] =SeriesProduct(a0,a,b0,b,SeriesOrder*mm);
b(SeriesOrder*mm+1:NMoments*SeriesOrder+1)=0;
end
% b0
% b
%str=input('Look at numbers')
EXZ(mm+1,1)=b0;
for pp2=1:SeriesOrder*mm
EXZ(mm+1,1)=EXZ(mm+1,1)+b(pp2).*EZ(pp2);
end
for pp1=1:NZterms
EXZ(mm+1,pp1+1)=b0.*EZ(pp1);
for pp2=1:SeriesOrder*mm
EXZ(mm+1,pp1+1)=EXZ(mm+1,pp1+1)+b(pp2).*EZ(pp2+pp1);
end
end
end
%u1=EXZ(2,1);
u2=EXZ(3,1);
if(NMoments>=3)
u3=EXZ(4,1);
end
%NMoments
if(NMoments>=4)
u4=EXZ(5,1);
end
u1=a0+a(2);
if(SeriesOrder>=4)
u1=a0+a(2)+3*a(4);
end
if(SeriesOrder>=6)
u1=u1+15*a(6);
end
if(SeriesOrder>=8)
u1=u1+105*a(8);
end
%k2=u2-u1^2;
%k3=u3-3*u2*u1+2*u1^3;
%k4=u4-4*u3*u1-3*u2^2+12*u2*u1^2-6*u1^4;
du1(1)=1;%----2
% du1(2)=0;%----2
% du1(3)=1;%----2
% du1(4)=0;%----2
% du1(5)=1;%----2
% du1(6)=0;%----2
% du1(7)=15;%----2
% du1(8)=0;%----2
% du1(9)=105;%----2
% du1(10)=0;%----2
du2(1)=2*EXZ(2,1);
if(NMoments>=3)
du3(1)=3*EXZ(3,1);
end
if(NMoments>=4)
du4(1)=4*EXZ(4,1);
end
%du1(1)=1;%----2
%du2(1)=0;
%du3(1)=0;
%du4(1)=0;
for mm=2:SeriesOrder+1
du1(mm)=EXZ(1,mm);
du2(mm)=2*EXZ(2,mm);
if(NMoments>=3)
du3(mm)=3*EXZ(3,mm);
end
if(NMoments>=4)
du4(mm)=4*EXZ(4,mm);
end
end
if(NMoments>=5)
u5=EXZ(6,1);
%du5(1)=5*EXZ(5,1);
for mm=1:SeriesOrder+1
du5(mm)=5*EXZ(5,mm);
end
end
if(NMoments>=6)
u6=EXZ(7,1);
%du6(1)=0;
for mm=1:SeriesOrder+1
du6(mm)=6*EXZ(6,mm);
end
end
if(NMoments>=7)
u7=EXZ(8,1);
%str=input('Look at k7 and k71')
%du7(1)=0;
for mm=1:SeriesOrder+1
du7(mm)=7*EXZ(7,mm);
end
end
if(NMoments>=8)
u8=EXZ(9,1);
for mm=1:SeriesOrder+1
du8(mm)=8*EXZ(8,mm);
end
end
if(NMoments>=9)
u9=EXZ(10,1);
for mm=1:SeriesOrder+1
du9(mm)=9*EXZ(9,mm);
end
end
if(NMoments>=10)
u10=EXZ(11,1);
for mm=1:SeriesOrder+1
du10(mm)=10*EXZ(10,mm);
end
end
F(1,1)=u1-Ms(1);
F(2,1)=u2-Ms(2);
F(3,1)=u3-Ms(3);
if(NMoments>=4)
F(4,1)=u4-Ms(4);
end
if(NMoments>=5)
F(5,1)=u5-Ms(5);
end
if(NMoments>=6)
F(6,1)=u6-Ms(6);
end
if(NMoments>=7)
F(7,1)=u7-Ms(7);
end
if(NMoments>=8)
F(8,1)=u8-Ms(8);
end
if(NMoments>=9)
F(9,1)=u9-Ms(9);
end
if(NMoments>=10)
F(10,1)=u10-Ms(10);
end
for mm=1:SeriesOrder+1
dF(1,mm)=du1(mm);
dF(2,mm)=du2(mm);
dF(3,mm)=du3(mm);
if(NMoments>=4)
dF(4,mm)=du4(mm);
end
if(NMoments>=5)
dF(5,mm)=du5(mm);
end
if(NMoments>=6)
dF(6,mm)=du6(mm);
end
if(NMoments>=7)
dF(7,mm)=du7(mm);
end
if(NMoments>=8)
dF(8,mm)=du8(mm);
end
if(NMoments>=9)
dF(9,mm)=du9(mm);
end
if(NMoments>=10)
dF(10,mm)=du10(mm);
end
end
end
.
.
Code: Select all
function [ObjMomentOut] = CalculateObjMoment(Moment0,Moment,w,MOrder)
ObjMomentOut=0;
for nn=1:MOrder
ObjMomentOut=ObjMomentOut+(Moment(nn)-Moment0(nn)).^2.*w(nn);
end
end
.
.
.
Code: Select all
function [mu1,cMu] = ConvertRawMomentsToCentralMoments(Mu,mOrder)
%cu
%mu
% %mOrder
%str=input('Look at numbers');
mu1=Mu(1);
for mm=2:mOrder
cMu(mm)=0;
for jj=0:mm
if(jj==0)
cMu(mm)=cMu(mm)+ (-1)^(mm-jj).*factorial(mm)/factorial(jj)/factorial(mm-jj)*1*mu1.^(mm-jj);
else
cMu(mm)=cMu(mm)+ (-1)^(mm-jj).*factorial(mm)/factorial(jj)/factorial(mm-jj)*Mu(jj)*mu1.^(mm-jj);
end
end
end
.
.
.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, when we fix the conditional 1D Z-series density by altering the six moments, the density takes a slight tilt towards the left(in some cases that I ran). Today, I am trying to see whether this tilt can also be fixed. I am very hopeful that we would soon be able to get more faithful densities without any such tilt. Let us see how this effort goes. If it works, I will post a new program tonight.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, my experiment with further improving the density did not work. However, I noticed that performing too many iterations of Newton causes a worse density. I kept Newton iterations to 500 only and was able to get the program to work only for 10000 paths. Here are some graphs with same parameters as yesterday but with only 10000 paths(as opposed to 25000 paths yesterday) and the conditional densities are still good.
Here are some graphs with 10,000 paths (with only 500 Newton iterations).
.
.
.
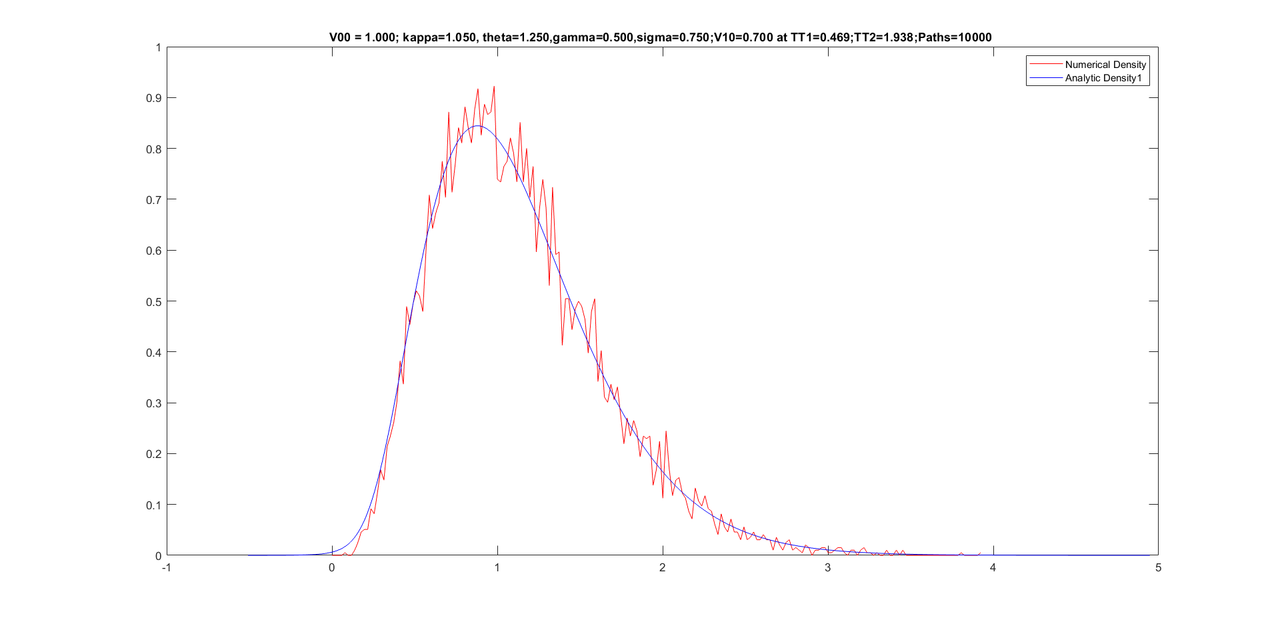
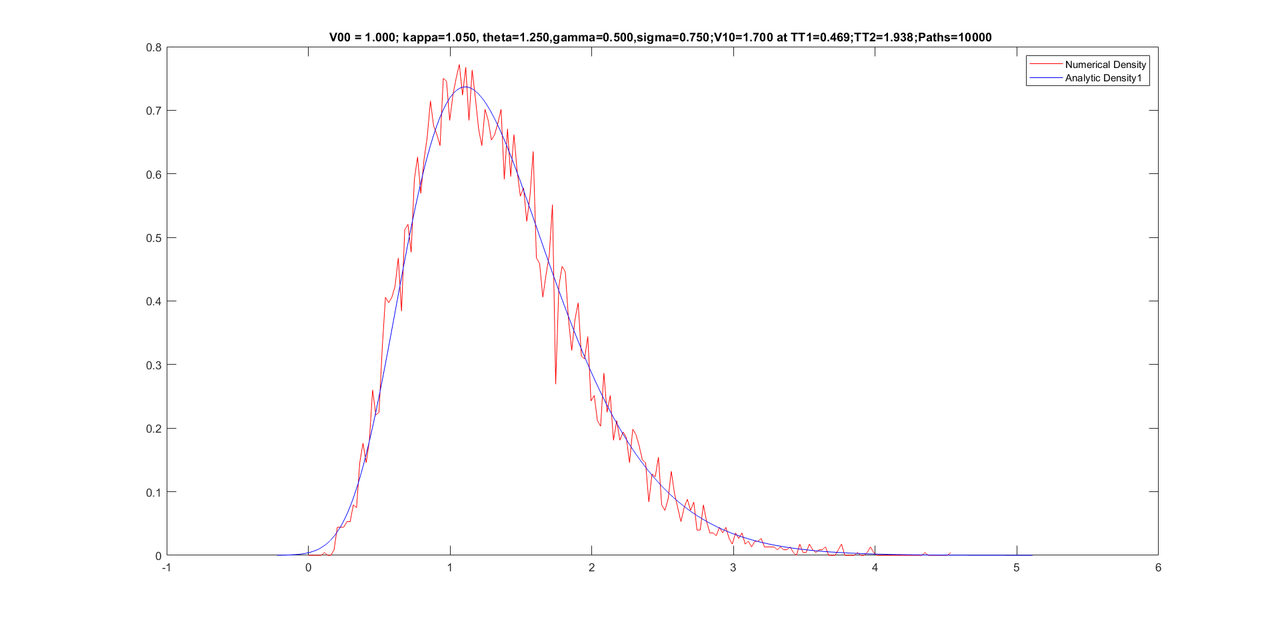
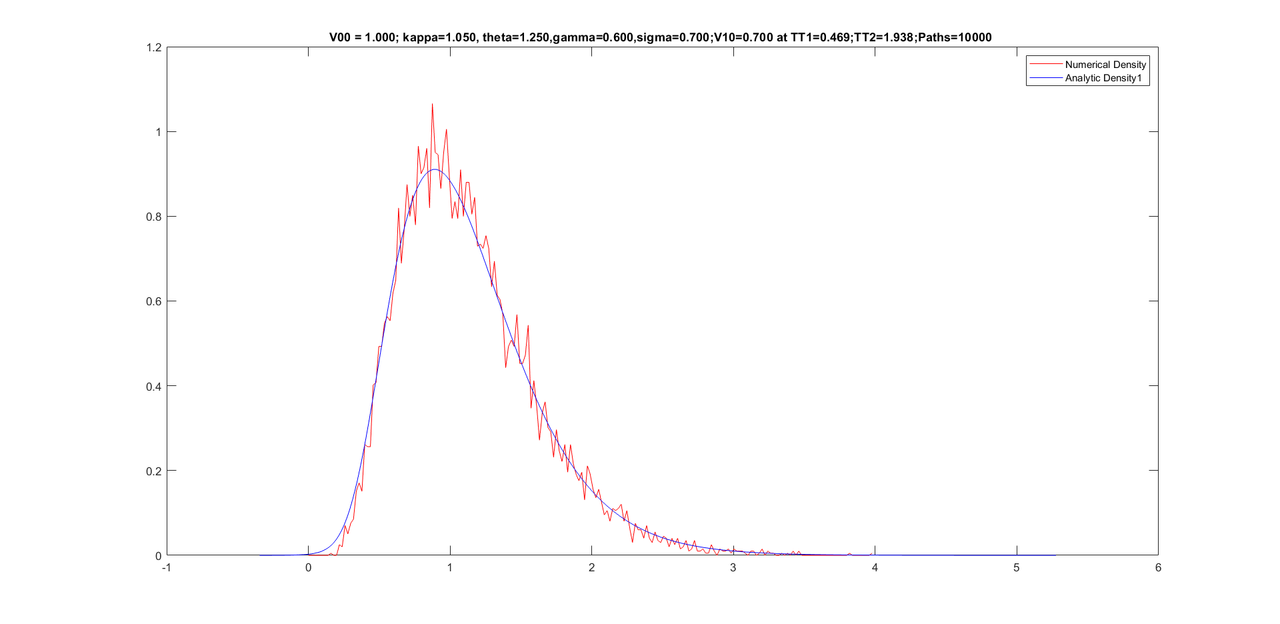
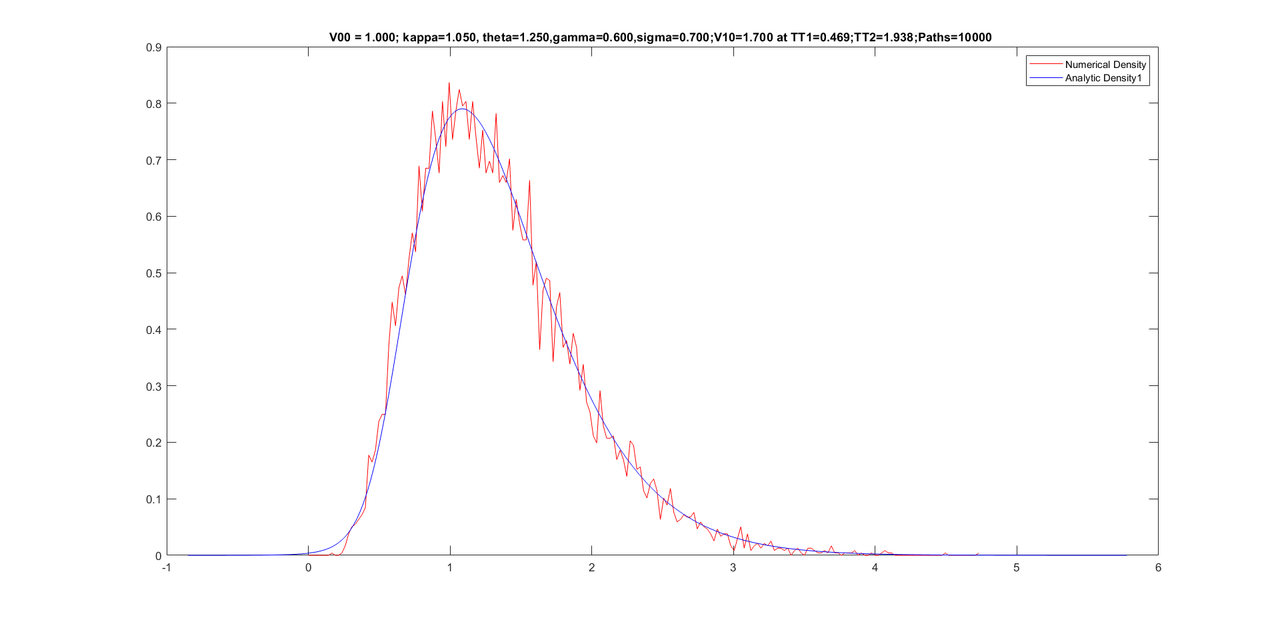
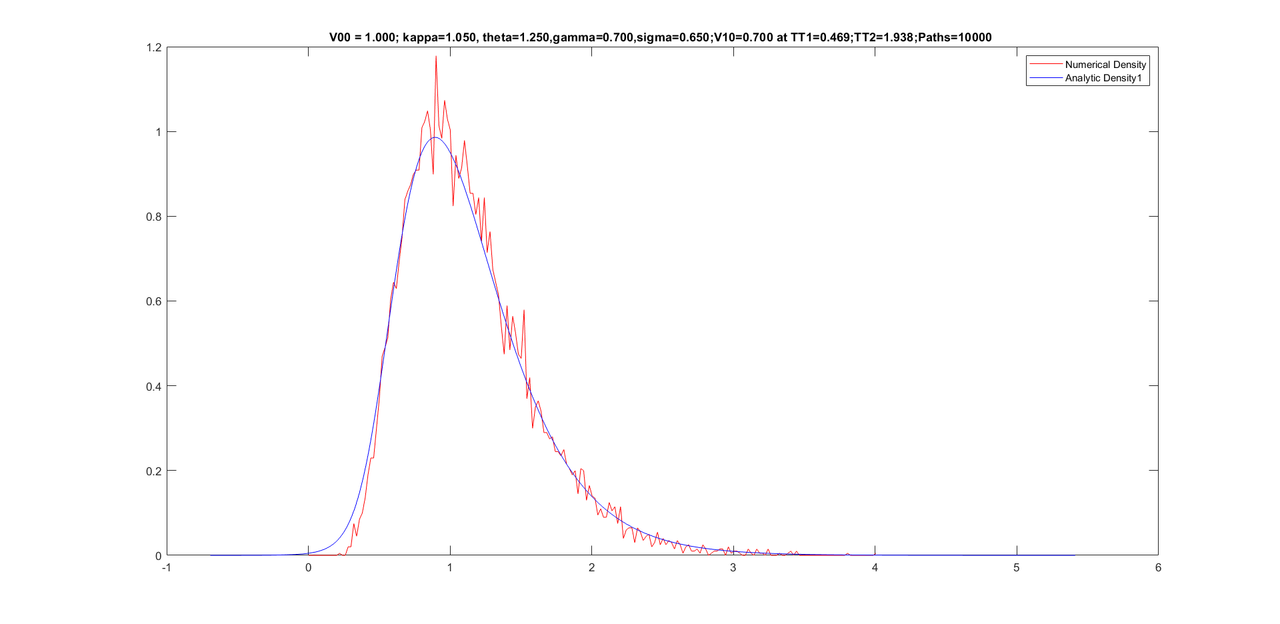
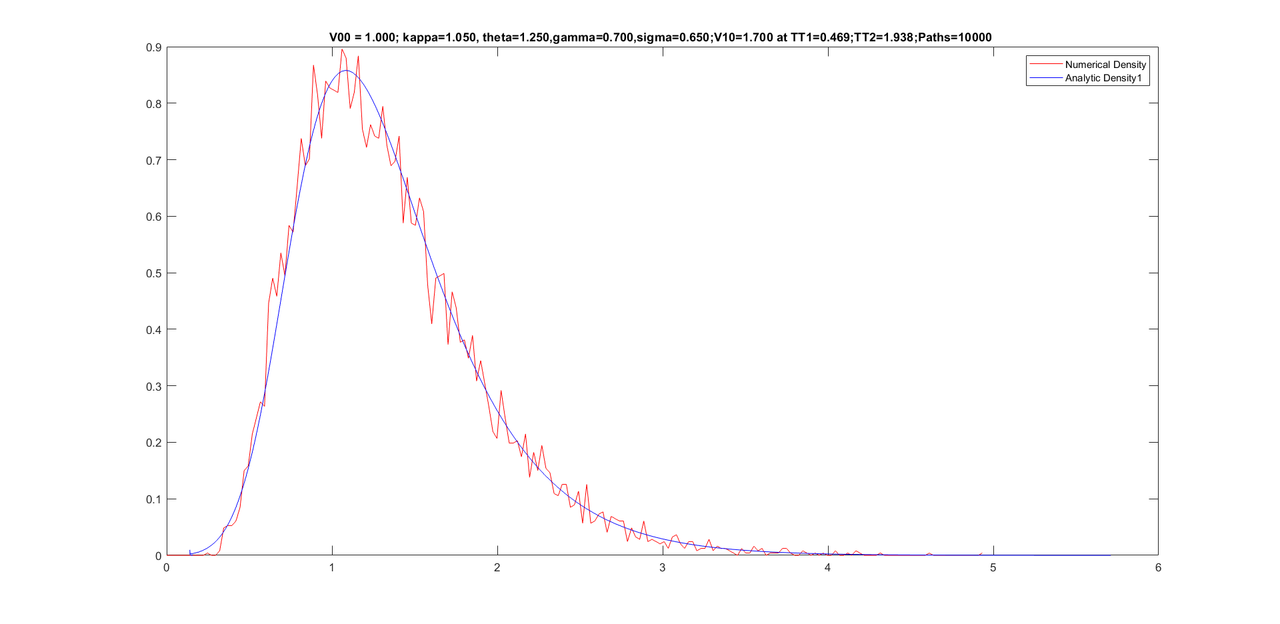
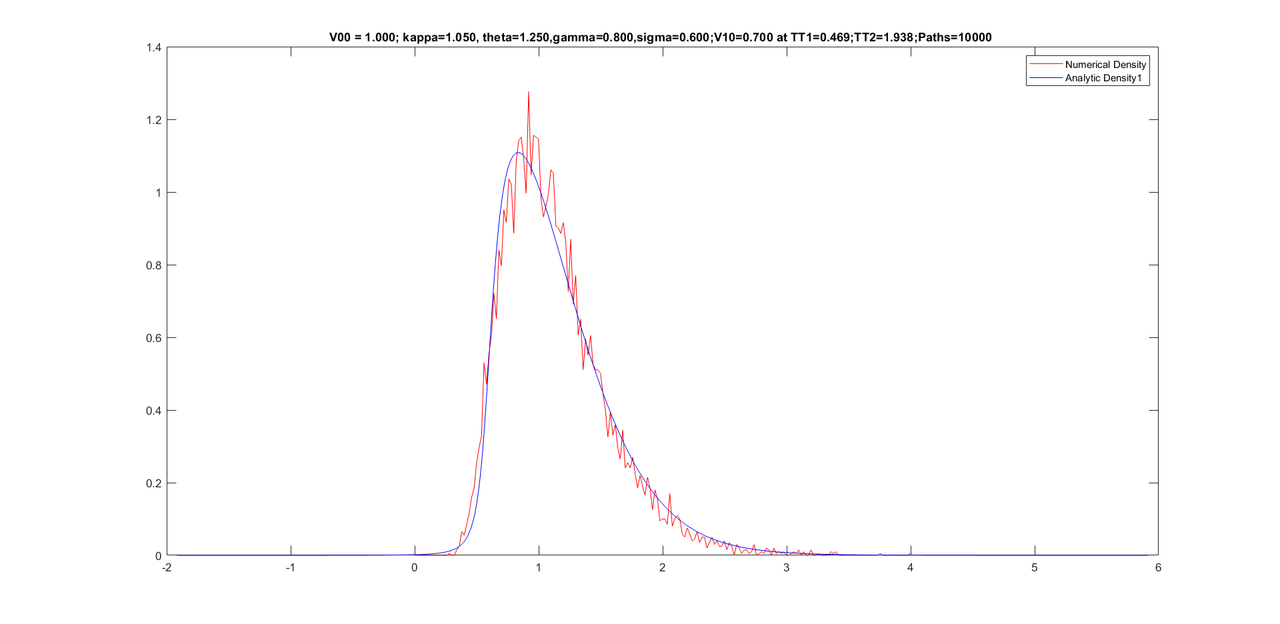
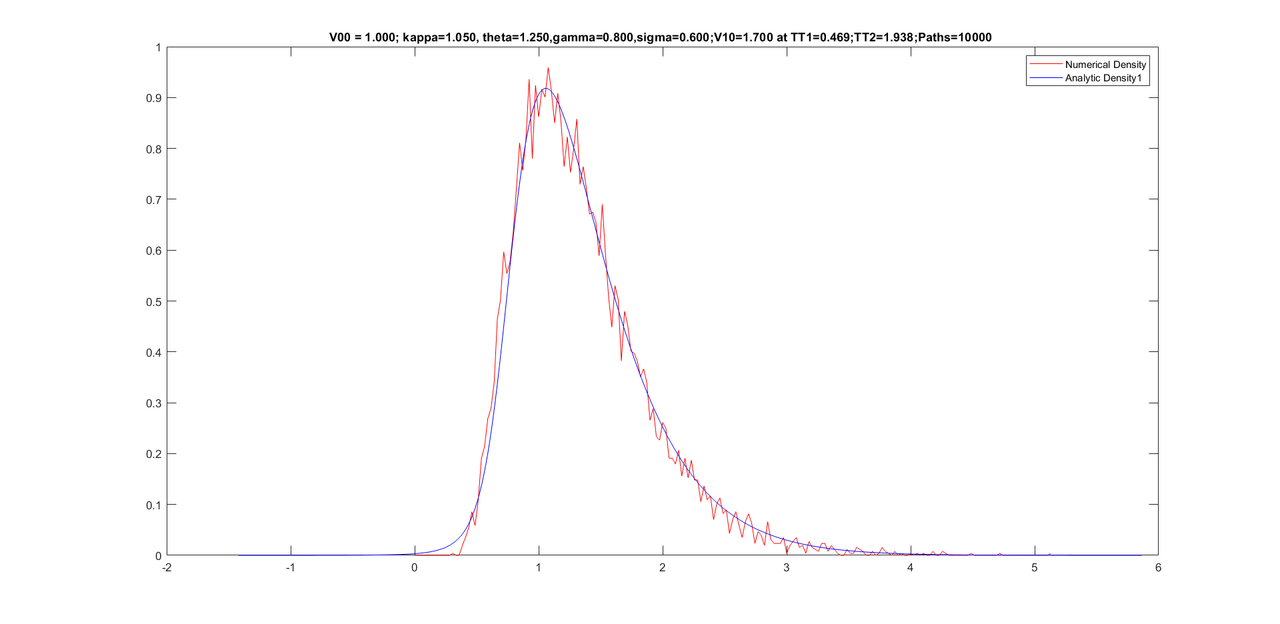
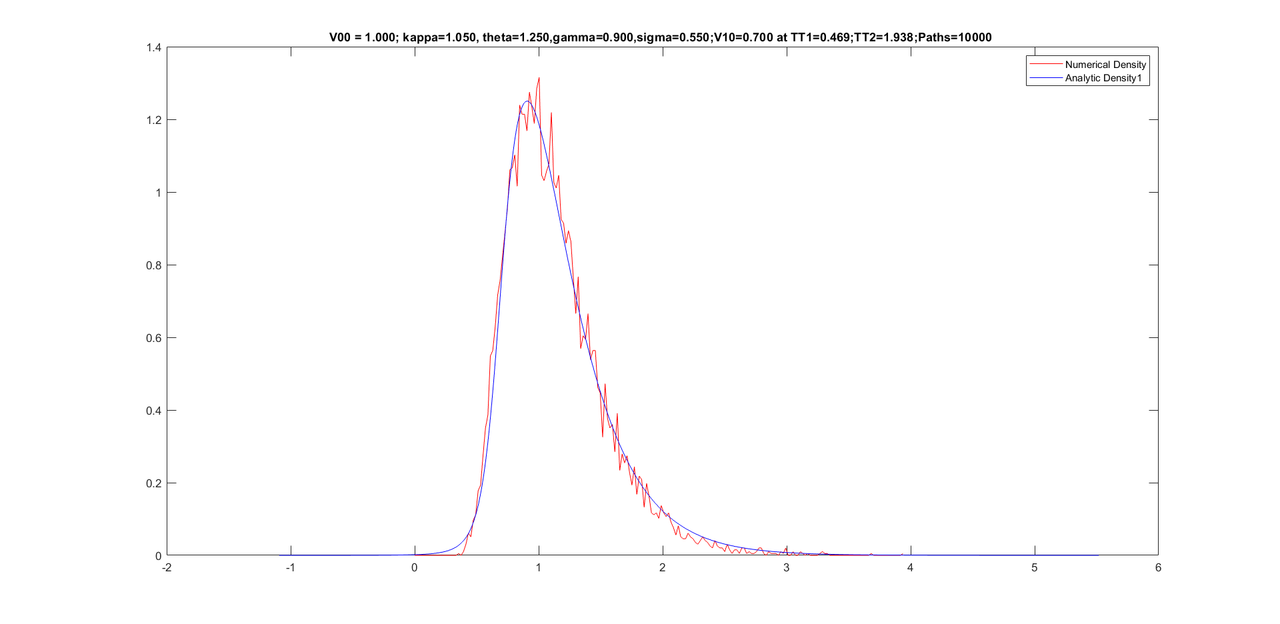
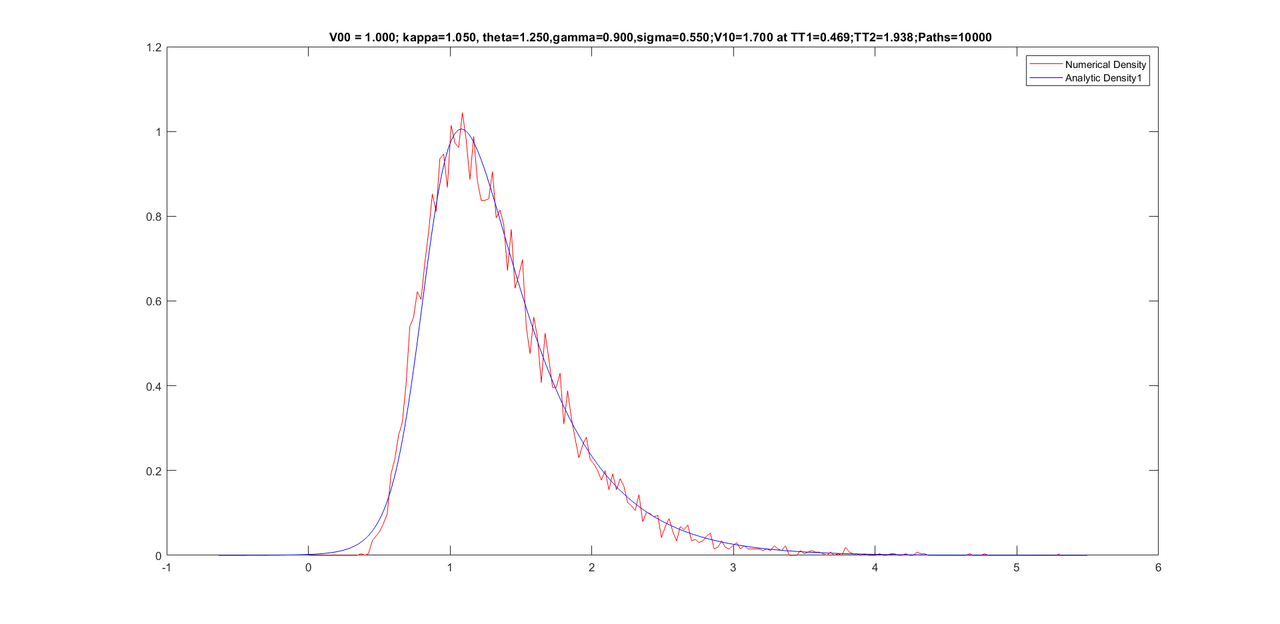
Here are some graphs with 10,000 paths (with only 500 Newton iterations).
.
.
.










You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Here is the slightly modified matlab program. I used this program to make conditional densities in previous post with 10000 paths.
.
.
.
.
.
.
Code: Select all
function []= ConditionalDensityHermitesBivariateNewtonIters02()
%SV SDE is
%dV(t)=mu1 V(t)^beta1 dt+ mu2 V(t)^beta2 dt + sigma0 V(t)^gamma dZ(t)
%In mean reverting SDEs we ususally have
%mu1= kappaV * thetaV
%beta1=0
%mu2=-kappa
%beta2=0
%NDim=4;%Three assets and one SV.
%%%%%%%%%%%%%%%%%%%5
V0=1.00;%.32;
V00=V0;
thetaV=1.250;%.045;%1;%.04;
kappaV=1.05;%1.5;%1.5;
mu1=kappaV*thetaV;
mu2=-kappaV;
beta1=0;
beta2=1;
gamma=.9;%.950;
sigma0=.55%.45;%
dt=.03125/2;
Tt=64*2;
T=Tt*dt;
seed0=52130649;
rng(seed0, 'twister')
paths=10000;
V(1:paths,1)=V0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
TT1=30; %Transition distribution start
TT2=124; %Transition distribution end
Random2(1:paths/2,1)=0;
for tt=1:Tt
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
if(tt==TT1)
Xin(1:paths,1)=V(1:paths,1);
end
if(tt==TT2)
Yin(1:paths,1)=V(1:paths,1);
end
end
str=input("I have reached stone 1");
Order=5;
%The function below does initial analytics of caclulation of 2D conditional
%and joint densities. We want to use the result from this function as a
%Starting guess/seed to Newton derivatives based optimization method.
[YCoeffHH,XYCoeffHH,XCoeffH,Coeffyx,YCoeffH] =CalculateBivariateHermiteSeries01(Yin,Xin,Order);
for qq1=1:Order+1
XMoments(qq1)=sum(Xin(1:paths).^qq1)/paths;
end
[XCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(XCoeffH(1:Order+1),Order);
[XCoeffZ(1),XCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(XMoments,XCoeffZ(2:6));
for pp1=1:Order+1
YMoments(pp1)=sum(Yin(1:paths).^pp1)/paths;
end
[YCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffH(1:Order+1),Order);
[YCoeffZ(1),YCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YMoments,YCoeffZ(2:6));
[YCoeffH] = ConvertZSeriesToHermiteSeriesNew(YCoeffZ,Order);
YCoeffHH(1:Order+1,Order:Order+1)=YCoeffHH(1:Order+1,Order:Order+1)/100000;
YCoeffHH(Order:Order+1,1:Order+1)=YCoeffHH(Order:Order+1,1:Order+1)/100000;
%The above 2D Conditional density calculated from regression is used as an
%input seed to Newton method. YCoeffHH is input as a seed to Newton method
%after converting it to a 2D Z-series.
str=input("I have reached stone 2");
%Below, we calculate Target cross-moments of Y and X from data.
for pp1=1:Order+1
for qq1=1:Order+1
MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Yin(1:paths).^pp1.*Xin(1:paths).^qq1)/paths;
end
end
% for pp1=1:Order+1
% pp4=6;
% pp3=5;
% pp2=4;
% pp1=3;
% if((MomentsYX0((pp4-1)*(Order+1)+qq1,1)/MomentsYX0((pp3-1)*(Order+1)+qq1,1))<(MomentsYX0((pp2-1)*(Order+1)+qq1,1)/MomentsYX0((pp1-1)*(Order+1)+qq1,1)))
% MomentsYX0((pp4-1)*(Order+1)+qq1,1)=MomentsYX0((pp3-1)*(Order+1)+qq1,1)*(MomentsYX0((pp2-1)*(Order+1)+qq1,1)/MomentsYX0((pp1-1)*(Order+1)+qq1,1));
%
% str=input("Moments are being altered")
% end
% %for qq1=1:Order+1
% % MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Yin(1:paths).^pp1.*Xin(1:paths).^qq1)/paths;
% %end
% end
%Before we enter Newton optimization function, we want to convert 2D and 1D hermite
%Series to Z-series.
[XCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(XCoeffH(1:Order+1),Order);
[YCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffH(1:Order+1),Order);
[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
OrderY=Order;
OrderX=Order;
[Y1DMoments]=CalculateMomentsOfZSeries(YCoeffZ(1),YCoeffZ(2:6),5,6)
MaxIter0=30;
YCoeffZZ=CalculateSmoothingGuessDensity2D(YCoeffZZ,XCoeffZ,MomentsYX0,Y1DMoments,OrderY,OrderX,MaxIter0)
str=input("Look at smoothing results")
MaxIter=500;
[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeries(YCoeffZZ,XCoeffZ,Order,MomentsYX0,Y1DMoments,MaxIter);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
% Order=7
% YCoeffHH(1:Order+1,Order:Order+1)=0.0;%YCoeffHH(1:Order+1,Order:Order+1)/100000;
% YCoeffHH(Order:Order+1,1:Order+1)=0.0;%YCoeffHH(Order:Order+1,1:Order+1)/100000;
%
% for pp1=1:Order+1
% for qq1=1:Order+1
% MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Yin(1:paths).^pp1.*Xin(1:paths).^qq1)/paths;
% end
% end
%
%MaxIter0=30;
%YCoeffZZ=CalculateSmoothingGuessDensity2D(YCoeffZZ,XCoeffZ,MomentsYX0,Y1DMoments,OrderY,OrderX,MaxIter0);
%str=input("Look at smoothing results")
%MaxIter=200;
%[YCoeffZZ,AMat] = DoNewtonIterationsOn2DZSeries(YCoeffZZ,XCoeffZ,Order,MomentsYX0,Y1DMoments,MaxIter);
%YCoeffZZ is the 2D conditional Z-series of Y given X [Y|X](Zy,Zx)
%that is the result of optimization method and is calibrated to Cross-moments of Y and X.
%MaxIter0=30;
%YCoeffZZ=CalculateSmoothingGuessDensity2D(YCoeffZZ,XCoeffZ,MomentsYX0,Y1DMoments,OrderY,OrderX,MaxIter0);
%str=input("Look at smoothing---3 results")
OrderY=Order;
OrderX=Order;
NMoments=6;
[MeanZZ,VarZZ] = CalculateMeanAndVarOf2DZSeriesY(YCoeffZZ,OrderY,OrderX)
%The name of above function is slightly misleading. It calculates mean and
%second moment
[Y1DMoments]=CalculateMomentsOfZSeries(YCoeffZ(1),YCoeffZ(2:6),5,6)
[YMoments] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,OrderY,OrderX,NMoments);
Y1DMoments
YMoments
%Y1DMoments(2)-Y1DMoments(1).^2
%VarZZ
str=input("Look at comparison of second moments/moments");
YCoeffZZ
%AMat
%MomentsYX0
%Below Check the difference between model moments and target moments.
%AMat-MomentsYX0
%Below, we convert the 2D Conditional Z-series of [Y|X](Zy,Zx) into 2D
%Conditional Hermite Seiries of [Y|X](Zy,Zx).
[YCoeffHH] = ConvertZSeriesToHermiteSeries2D(YCoeffZZ,Order+1,Order+1)
% MMul1=sqrt(YCoeffHH(1,1).^2+YCoeffHH(1,2).^2+YCoeffHH(1,3).^2*2+YCoeffHH(1,4).^2*6+YCoeffHH(1,5).^2*24+YCoeffHH(1,6).^2*120)
% YCoeffH(1)
%
% YCoeffHH(1,:)=YCoeffHH(1,:)*abs(YCoeffH(1))./MMul1;
%
%
% MMul2=sqrt(YCoeffHH(2,1).^2+YCoeffHH(2,2).^2+YCoeffHH(2,3).^2*2+YCoeffHH(2,4).^2*6+YCoeffHH(2,5).^2*24+YCoeffHH(2,6).^2*120)
% YCoeffH(2)
%
% MMul3=sqrt(YCoeffHH(3,1).^2+YCoeffHH(3,2).^2+YCoeffHH(3,3).^2*2+YCoeffHH(3,4).^2*6+YCoeffHH(3,5).^2*24+YCoeffHH(3,6).^2*120)
% YCoeffH(3)
%
%
% MMul4=sqrt(YCoeffHH(4,1).^2+YCoeffHH(4,2).^2+YCoeffHH(4,3).^2*2+YCoeffHH(4,4).^2*6+YCoeffHH(4,5).^2*24+YCoeffHH(4,6).^2*120)
% YCoeffH(4)
%
% MMul5=sqrt(YCoeffHH(5,1).^2+YCoeffHH(5,2).^2+YCoeffHH(5,3).^2*2+YCoeffHH(5,4).^2*6+YCoeffHH(5,5).^2*24+YCoeffHH(5,6).^2*120)
% YCoeffH(5)
%
%
% MMul6=sqrt(YCoeffHH(6,1).^2+YCoeffHH(6,2).^2+YCoeffHH(6,3).^2*2+YCoeffHH(6,4).^2*6+YCoeffHH(6,5).^2*24+YCoeffHH(6,6).^2*120)
% YCoeffH(6)
%YCoeffHH(1,:)=YCoeffHH(1,:)*abs(YCoeffH(1))./MMul1;
%YCoeffHH(2,:)=YCoeffHH(2,:)*abs(YCoeffH(2))./MMul2;
%YCoeffHH(3,:)=YCoeffHH(3,:)*abs(YCoeffH(3))./MMul3;
%YCoeffHH(4,:)=YCoeffHH(4,:)*abs(YCoeffH(4))./MMul4;
%YCoeffHH(5,:)=YCoeffHH(5,:)*abs(YCoeffH(5))./MMul5;
%YCoeffHH(6,:)=YCoeffHH(6,:)*abs(YCoeffH(6))./MMul6;
%
%
%
%
% str=input("Look at comparison of coefficients")
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%In this block, we do conditional Monte Carlo of SDE which is the true
%numerical 1D conditional density of Y conditional on X having a given
%value. This value of X on which we are conditionin is defined by V10 below.
%We can alter V10 below and it will take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
V10=1.70;
V(1:paths)=V10;
Random2(1:paths,1)=0;
for tt=TT1+1:TT2
Random2(1:paths/2)=randn(paths/2,1);
Random2(paths/2+1:paths)=-Random2(1:paths/2);
V(1:paths,1)=V(1:paths,1)+ ...
(mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
(mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
.5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...
sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
.5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;
V(V<0)=.00001;
end
%Below
NoOfBins=200;
MaxCutOff=10;
[XDensity,IndexOut,IndexMax] = MakeDensityFromSimulation_Infiniti_NEW(V,paths,NoOfBins,MaxCutOff );
clf;
plot(IndexOut(1:IndexMax),XDensity(1:IndexMax),'r');
hold on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%Below, we calculate the value of Zx0 corresponding to X0 (here V10). This
%comes from inverting the Z-series of X so that X=V10;
xOrder=Order;
yOrder=Order;
[Zx0] = CalculateZgivenXAndHSeriesCoeffs(V10,XCoeffH,xOrder);
%Below, we collapse two dimensional pdf of Y|X to one dimensional pdf given
%Zx i.e. this Y|X=X(Zx)
%Here we take out a 1D slice from the 2D density
%of Y conditional on X taking a specific value (here V10).
He(1)=1;
He(2)=Zx0;
He(3)=Zx0^2-1;
He(4)=Zx0^3-3*Zx0;
He(5)=Zx0^4-6*Zx0.^2+3;
He(6)=Zx0^5-10*Zx0.^3+15*Zx0;
He(7)=Zx0^6-15*Zx0.^4+45*Zx0.^2-15;
He(8)=Zx0^7-21*Zx0.^5+105*Zx0.^3-105*Zx0;
YCoeffh(1:Order+1)=0;
for hh=1:yOrder+1
for hh2=1:xOrder+1
YCoeffh(hh)=YCoeffh(hh)+YCoeffHH(hh,hh2).*He(hh2);
end
end
[YCoeffz(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffh(1:Order+1),Order);
%
%
% %[IsValidFlag] = CheckIsValidDensityPN(YCoeffz(1),YCoeffz(2:Order+1));
% [PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(YCoeffz(1),YCoeffz(2:Order+1));
% PIsValidFlag
% NIsValidFlag
%
%
% for mm=1:100
% [PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(YCoeffz(1),YCoeffz(2:Order+1));
% if((NIsValidFlag==0)&&(PIsValidFlag==1))
% YCoeffz(5)=YCoeffz(5)-.01*abs(YCoeffz(5));
% YCoeffz(6)=YCoeffz(6)+.001*abs(YCoeffz(6));
% %YCoeffz(3)=YCoeffz(3)-.001*abs(YCoeffz(3));
% end
%
% if((PIsValidFlag==0)&&(NIsValidFlag==1))
% YCoeffz(5)=YCoeffz(5)+.01*abs(YCoeffz(5));
% YCoeffz(6)=YCoeffz(6)+.001*abs(YCoeffz(6));
% %YCoeffz(3)=YCoeffz(3)-.001*abs(YCoeffz(3));
% end
%
% if((NIsValidFlag==0)&&(PIsValidFlag==0))
% YCoeffz(6)=YCoeffz(6)+.01*abs(YCoeffz(6));
% %YCoeffz(3)=YCoeffz(3)-.001*abs(YCoeffz(3));
% end
%
% end
%
% [YCoeffh] = ConvertZSeriesToHermiteSeriesNew(YCoeffz,Order)
%
PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh(2:yOrder+1),'b')
%hold on
%PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh1(2:yOrder+1),'g')
title(sprintf('V00 = %.3f; kappa=%.3f, theta=%.3f,gamma=%.3f,sigma=%.3f;V10=%.3f at TT1=%.3f;TT2=%.3f;Paths=%d ',V00, kappaV, thetaV,gamma,sigma0, V10,(TT1*dt),(TT2*dt),paths));%,sprintf('theta= %f', theta), sprintf('kappa = %f', kappa),sprintf('sigma = %f', sigma0),sprintf('T = %f', T));
legend({'Numerical Density','Analytic Density1'}, ...
'Location','northeast')
str=input("This is the first version without altering the moments of conditional density")
[YMoments0]=CalculateMomentsOfZSeries(YCoeffz(1),YCoeffz(2:6),5,6)
% %[IsValidFlag] = CheckIsValidDensityPN(YCoeffz(1),YCoeffz(2:Order+1));
[PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(YCoeffz(1),YCoeffz(2:Order+1));
PIsValidFlag
NIsValidFlag
LoopIter=0;
Mul6(1)=.65;
Mul6(2)=.7;
Mul6(3)=.75;
Mul6(4)=.8;
Mul6(5)=.85;
Mul6(6)=.9;
Mul6(7)=.95;
Mul6(8)=1.0;
Mul6(9)=1.05;
Mul6(10)=1.1;
Mul0=1;
YMoment6=YMoments(6);
while(((PIsValidFlag==0)||(NIsValidFlag==0))&&(LoopIter<=10))
LoopIter=LoopIter+1;
YCoeffh
Mul0=Mul0+.05;
Y2Coeffz=YCoeffz;
Mean=Y2Coeffz(1)+(Y2Coeffz(3)+3*Y2Coeffz(5));
Y2Coeffz(1)=-(Y2Coeffz(3)+3*Y2Coeffz(5));
[YMoments]=CalculateMomentsOfZSeries(Y2Coeffz(1),Y2Coeffz(2:6),5,6)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%abs(YMoments(3:6))./abs(YMoments(2:5))
%YMoments(2:6)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%555
if(abs(YMoments(6)/YMoments(5))<abs(YMoments(4)/YMoments(3))*Mul6(LoopIter))
YMoments(6)=abs(YMoments(5).*YMoments(4)./YMoments(3)*Mul6(LoopIter))
end
%YMoments(6)=YMoments(6)*Mul0;
%LoopIter
%Mul0
%YMoments(6)
%str=input("Look at variables")
[Y3Coeffz(1),Y3Coeffz(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YMoments,Y2Coeffz(2:6));
Y3Coeffz(1)=Mean-(Y2Coeffz(3)+3*Y2Coeffz(5));
[PIsValidFlag,NIsValidFlag] = CheckIsValidDensityPN02(Y3Coeffz(1),Y3Coeffz(2:Order+1));
PIsValidFlag
NIsValidFlag
end
if(LoopIter==0)
Y3Coeffz=YCoeffz;
end
clf;
plot(IndexOut(1:IndexMax),XDensity(1:IndexMax),'r');
hold on
PlotZSeriesDensity(Y3Coeffz(1),Y3Coeffz(2:yOrder+1),'b')
title(sprintf('V00 = %.3f; kappa=%.3f, theta=%.3f,gamma=%.3f,sigma=%.3f;V10=%.3f at TT1=%.3f;TT2=%.3f;Paths=%d ',V00, kappaV, thetaV,gamma,sigma0, V10,(TT1*dt),(TT2*dt),paths));%,sprintf('theta= %f', theta), sprintf('kappa = %f', kappa),sprintf('sigma = %f', sigma0),sprintf('T = %f', T));
legend({'Numerical Density','Analytic Density1'}, ...
'Location','northeast')
str=input("This is the Second version after possibly altering the moments of conditional density when needed")
endYou think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I have been away from my research on 2D Hermite-series for past two days and have rather been trying to debug my market trading program written in python. I hope to get back to my research tomorrow. I am under intense pressure from within myself and from the family and the psychiatrist to be able to make money on my own and I have to continue that work from time to time. Despite these occasional breaks, I want to say that I am into 2D and multidimensional hermite series research for months or possibly years to come. I am in it for a long haul and occasional breaks will not stop my research. I want to be in the research on probability theory for the rest of my life.
On this weekend, I will explain all the basics and other details of my research on 2D Hermite-series with latex equations. I will also look for more ideas to make the optimization program more robust but I will have to think of some different ideas for that.
I hope that I am mostly done with my market trading program and it only needs tweaking from time to time so in coming weeks, I will be spending most of my time on 2D hermite-series research. I really hope that we would do some interesting work over these coming winters.
On this weekend, I will explain all the basics and other details of my research on 2D Hermite-series with latex equations. I will also look for more ideas to make the optimization program more robust but I will have to think of some different ideas for that.
I hope that I am mostly done with my market trading program and it only needs tweaking from time to time so in coming weeks, I will be spending most of my time on 2D hermite-series research. I really hope that we would do some interesting work over these coming winters.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I have been thinking about the problem of fitting cross-moments and 1D moments on a 2D Z-series and I am afraid that Newton is not the best possible solution here.
I had the idea that we could fit the coefficients on a Z-series so that they fit the moments with multi-dimensional bisection. We have to choose an objective function that has (monotonically) positive or negative derivatives with respect to coefficients. And Moments increase monotonically with increase in coefficients. Suppose, we can estimate the valid range for each coefficient in advance and the coefficient would be known to exist in that range. We have to bisect along the diagonal of hyper-plane of the range of parameters. I think, along the diagonal, if there are N dimensions (or N parameters), we can eliminate the hyper-cube volume (where coefficient cannot be found or where coefficient can actually be found depending upon which side of our multi-dimensional bisection the target value of objective function lies) at a rate of 1/N^2 by doing one bisection along the diagonal of hyper-plane of valid ranges of all variables. Later depending upon how it turns out, our valid hyper-plane where the target objective function lies can take all sort of interesting shapes (In two dimensions, it can be an L-shaped area) and we have to make simple rules about how to proceed in different dimensions. Computers are fast and I think we can solve the problem reasonably quickly on an ordinary computer.
Please give me a few days to work on the problem since I am afraid that we cannot rely on Newton to solve the problem universally and we need something more interesting to be able to solve the given problem. Even though, there may be some difficulty I have not imagined, I hope that I would be able to write a program that solves for fitting of Z-series coefficients to cross-moments of even higher volatility stochastic processes.
I think many other optimization problems can be solved like this but underlying condition is that derivatives of the objective function should not switch sign and we might have to improvise to fulfill this condition. There might be some problems I have not thought of but I want to give this a try.
I had the idea that we could fit the coefficients on a Z-series so that they fit the moments with multi-dimensional bisection. We have to choose an objective function that has (monotonically) positive or negative derivatives with respect to coefficients. And Moments increase monotonically with increase in coefficients. Suppose, we can estimate the valid range for each coefficient in advance and the coefficient would be known to exist in that range. We have to bisect along the diagonal of hyper-plane of the range of parameters. I think, along the diagonal, if there are N dimensions (or N parameters), we can eliminate the hyper-cube volume (where coefficient cannot be found or where coefficient can actually be found depending upon which side of our multi-dimensional bisection the target value of objective function lies) at a rate of 1/N^2 by doing one bisection along the diagonal of hyper-plane of valid ranges of all variables. Later depending upon how it turns out, our valid hyper-plane where the target objective function lies can take all sort of interesting shapes (In two dimensions, it can be an L-shaped area) and we have to make simple rules about how to proceed in different dimensions. Computers are fast and I think we can solve the problem reasonably quickly on an ordinary computer.
Please give me a few days to work on the problem since I am afraid that we cannot rely on Newton to solve the problem universally and we need something more interesting to be able to solve the given problem. Even though, there may be some difficulty I have not imagined, I hope that I would be able to write a program that solves for fitting of Z-series coefficients to cross-moments of even higher volatility stochastic processes.
I think many other optimization problems can be solved like this but underlying condition is that derivatives of the objective function should not switch sign and we might have to improvise to fulfill this condition. There might be some problems I have not thought of but I want to give this a try.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
I really want to tell people that I have lived as a sane person due to support from friends otherwise I was even put to physical torture before my case got known to a lot of good people. I am copying an experience of planned physical abuse on the insistence of mind control agencies. I am copying context of the post as well.
The excerpt below is from a past post stating obvious abuse by various psychiatrists on the insistence of mind control agencies. The episode of physical abuse by beating me for more than twenty minutes is towards the end of this post:
Friends, I wanted to remain busy with my research and not speak about mind control and its reasons and people behind it. I simply wanted to concentrate on my research but whenever I have any progress in my research, my mind control and related torture sharply increases to make more research impossible for me. I want to remain totally devoted to my research and want friends to help me in doing that, I want everyone of all the good people in Europe or America who follow my research to please tell two or three journalists about my research and my mind control. I will also request European friends to ask their government and embassies to please keep a vigil about the matter and force corrupt Pakistani govt. and establishment to not drug food in Lahore with mind control chemicals.
I was a very simple, very meek but also very hard working student at a large university in New York and joined the university in 1997. My mind control started in very late 1997 when a racist jewish professor in Math department of my university was threatened by my talent and approached the Jewish Billionaire to ask American defense to put me under mind control. Even that long time ago, a large number of jews were very aware that this Jewish billionaire was a Godfather of mind control and would approach the billionaire to recommend talented people to mind control from time to time when they would be threatened by their talent. Over past twenty five years tens of thousands (if not more than a hundred thousand) of innocent people mostly American nationals have been placed on mind control abuse by scumbags of American defense on recommendation of Jewish billionaire. Most universities in US have a couple of jews who continue to keep eye on brilliant students of the university and recommend them to American defense through jewish billionaire when they feel threatened by the talent of the students due to any reason like their religion, race, ethnicity or just because they are not jews.
I had told friends earlier that a jewish billionaire is Godfather of mind control. When my persecution started (in late 1997) at the university in New York which is a big time player in mind control of Muslims, blacks and foreigners, many university officials were very pleased that they were getting written in good books of the billionaire jewish Godfather. Though there are far richer billionaires in US who are staunchly opposed to mind control, they are not ready to shell out hundreds of millions of dollars to bribe anyone to end mind control while mind control Godfather continues to give large bribes to people to continue mind control. Many of the people related to defense in mind control are given extremely high paying jobs in Godfather and his other jewish friends' companies after they retire from mind control and Godfather is extremely generous towards them and it is well established and well known to scum in mind control that after retarding muslims, blacks and others in their career, they will move to paradise(tens of people from army/Pentagon who follow whims of Billionaire Godfather are given jobs paying milllons of dollars by Godfather and his jewish cohort in several companies) after they retire. No wonder there is no let up in mind control whatever good people try.
We know in almost all classic folk lore stories evil is too strong and too sure of itself while good is mostly weak and just trying to protect itself from evil who is bent on damaging and eradicating the weak and the poor good but it is the weak and poor good that finally prevails. I want to tell good American friends that evil at this stage has become too bold and thousands of talented people are retarded every year. And it is just not muslims and blacks that are on the line, several thousands of brilliant whites are retarded across United States by mind control agency every year that has become too emboldened due to lack of any accountability. Thousands of foreigners are also kept retarded in dozens of countries including many European countries.
My only intention behind this post is that I want mind control to end from our societies. I do not have any joy in mentioning that there are some bad jewish actors behind it. In American society there are a large number of jews who have excelled in the professions of science, education, medicine and have made great contributions to our societies. There are a very large number of jewish professors each of whom would have taught tens of thousands of students on top of making extraordinary contributions to body of human knowledge through their great research. Then there are accomplished jewish scientists whose work, research and inventions make our everyday life better. There are great jewish doctors and surgeons who would treat countless sick people and make them recover from disease. The list of contributions of jewish people to humanity is very long and it continues. Then there are a large number of ordinary jewish folks who are known for their goodness and civility to other people in the society. When we know all of this, we do not want to say anything anti-jewish to hurt the feelings of so many good jewish people. But I still have to say there are really some bad people who are unconnected with most of the nice and accomplished jews and they instigate and continue cruel mind control torture on talented people of other ethnicities, religions and countries based on their personal dislike and hatred. My purpose is only to end the mind control victimization and torture on otherwise nice and talented people and I do not have any hidden intentions beyond that. And I am sure American society knows very well about the contributions of good Jews to both their country and broader humanity and my exposing some bad actors would never have any bad effect of any kind on these good and nice jews who we all respect and who are our role models.I want to tell friends something I have said before here that I am sure American society would eventually end the menace of mind control from their and other countries. I want to request all good Americans and Europeans to come forward and invite any investigative journalist you know to read my threads and ask them to help end the menace of mind control in our societies through their investigative journalism. Without any accountability evil will continue to grow stronger and then mind control would start to threaten even those people who consider themselves safe due to affiliations, status or wealth.
https://forum.wilmott.com/viewtopic.php?t=99702&start=2325#p881807
https://forum.wilmott.com/viewtopic.php?t=99702&start=2325#p881808
https://forum.wilmott.com/viewtopic.php?t=99702&start=2325#p881886
https://forum.wilmott.com/viewtopic.php?t=99702&start=2340#p881951
Friends, this speaks volumes about headstrong cruelty of people in American defense and their Jewish billionaire backers cohort that they are even more ready to show me cruelties even after people have a widespread knowledge of their machinations and tactics. These evil people have no intention or desire to decrease their torture on me despite that I have been telling tales of their inhuman torture on me over past twenty five years through various psychiatrists.
Please read the following two posts to see the context how I have been maltreated by various psychiatrists on behest of mind control agencies over past 25 years.
Friends, I have been on forced antipsychotics for most of the time since early 1999. There were a few periods of a few months when I remained free from antipsychotics. But other than two or three such periods, I have remained on antipsychotics. It is very hard to feel well when huge antipsychotics are forced on someone who is mentally healthy. I have also been detained forcefully tens of times whenever some of my neurotransmitters came back, the purpose of detention was to take brilliant neurotransmitters out of my brain and send me back home with a relatively retarded brain after the end of months long detentions. I have seen sheer trauma, torture and brutality on the hands of these psychiatrists who connive with American defense and Pakistani military to declare me mentally ill so they can force antipsychotics on me. I will be 51 this year and portion of my life that I lived under mind control has exceeded the part of early life that I lived without mind control.
I have a phone meeting with the psychiatrist on 14th of June 2024. And I am sure the psychiatrist will try again to keep me under medication or even increase my medication. Even after a large number of people have become aware of truth about mind control and accompanying persecution by the psychiatrists, most psychiatrists are not the least worried that their wrongdoing is being exposed in public.
I want to request good Americans to please protest to American defense, mind control agency, Pak army and relevant psychiatrists to please end this cruel practice of declaring healthy people on antipsychotics and forcefully detaining them up to years in their faciiities.
When they detain me, they have fixed all mind control gadgets and lasers in the psychiatric facility and they add all mind control chemicals openly in food and psychiatric drugs. It is a very controlled environment in captivity and within a month or so, they are able to remove all neurotransmitters from the brain of the victim. Every time I was detained, they kept me in the psychiatric facility for 30-50 days. One psychiatric even detained me for ten months after I returned from Britain. There are also instances of being detained for six months once and three months twice.
I really want to request American people again to please protest to their government and try to make sure that I am not being detained again on totally flimsy psychiatric grounds.
.
My Letter To HRW About My Human Rights Abuse
Above is a very incomplete account of how various psychiatrists continued to play in hands of Pakistan army to retard me. It also does not cover all the time till year 2022 and the account stops several years earlier. I could not write about last several years that were exceptionally brutal.
Friends, in a previous post I told friends how staff at a lady psychiatrist's hospital started beating me and abused me. During past twenty three years, there have been many many instances of my obvious abuse by different psychiatrists. I will describe some of those instances in this post.
When I came from United States and till fifteen years after that, my father would proudly ask me that I could see any psychiatrist I wish. This was because Pakistan army was managing my persecution and they would force psychiatrists to declare me schizophrenic and my father was told that every psychiatrist would be forced to cooperate. However, by chance in 2016, I came across a psychiatrist who was far better. I never told him that I was under mind control but whenever he interviewed me, he always said after the interview that I was perfectly sane and mentally healthy. When my family would force him to increase the dosage of antipsychotics, the doctor first told me that I should not live with my family and make a comprehensive plan to support myself and become independent (such a plan could never work since Pakistan army was threatening people in Pakistan to not give me any business and CIA was making sure that every contact I would reach for work in Europe (and Singapore/ Japan /Australia) would be approached by CIA telling them that I was a very bad guy and they must not do business with me. I had not told the doctor any such thing that intelligence agencies were after me.) When I told the good doctor how previous psychiatrists had abused me, he would tell me that this used to be a very widespread practice in America hundred years ago to wrong mentally healthy humans by using corrupt psychiatrists as instruments to detain them and strip them of their sanity. The good doctor I am talking about was American national with Pakistan background who had practiced psychiatry in America for over twenty years and had returned to Pakistan. That good doctor kept me on very low antipsychotics (1 mg resperidone per day) and that too on extreme insistence of my family. It was only during that time of treatment by that doctor that I got my first break in research and I solved the problem of high order monte carlo simulations (and analytic series solution of ODEs) and posted that solution on this thread. Ok, when my family was fed with the doctor, they detained me with another doctor. They detained me again two years ago when I requested my family that I wanted to see the same doctor of my choice again( I have been detained every year for past six or seven years by different doctors), they detained me through a different doctor. So my family now stubbornly refuses to allow me to see a professional qualified American psychiatrist of my own choice and detains me every time I try to approach him.
Now back to my obvious abuse by two other psychiatrists. I was detained by this doctor who was running a mental health facility and was not a psychiatrist himself. At that time I did not use to walk very much and my blood pressure used to be somewhat high. Since other antipsychotics had failed to retard me, doctor suggested I take aripperizole injections. These injections affect the heart and also elevate blood pressure but doctor who wanted to retard me had no regard for my health while pretending to cure me. In initial days of my detention, staff at the hospital when checked my blood pressure told me high enough blood pressure in line with what I used to have but after I complained about aripperizole and its effect on blood pressure the staff started doctoring blood pressure and started telling me that my blood pressure was very good or even low. This is a post I wrote on another thread in this forum about it. How to safeguard my research - Page 32 - wilmott.com
.
Later after a few days, I was given a second aripperizole injection and released from detention. An injection was due every fifteen days. My parents were in Saudi Arabia and I was living with my sister. She insisted after fifteen days that I get a new aripperizole injection. I complained about too much side effects and other serious problems but my sister insisted that I must get the injection. She talked to another doctor and the doctor told her that if his blood pressure and pulse are fine, just give him the injection. I asked my sister that my blood pressure must be checked before I get the new injection. We went to a small hospital close to her house and when my blood pressure was checked my lower blood pressure was 110. The hospital staff recommended that I stay at the hospital in their care until my blood pressure decreases. It was a totally random blood perssure check. When hospital staff came to know that I had been given aripperizole injections, they told my sister to not give me those injections any more. My sister asked the staff to relieve me and we came home but I was not given aripperizole injections after that.
But this is interesting that the psychiatrist was initially desperate to prescribe aripperizole despite that I had told him about my heart and blood pressure problems and his staff was asked to doctor blood pressure so that I would accept the injections.
Good thing is that only after stopping aripperizole, I started my treatment with good psychiatrist doctor Naeem Aftab (who is an American national) and he gave me enough relief that I was able to get a break in my research and solve the problem of high order monte carlo simulations. I would always be thankful to Dr. Naeem Aftab for giving me relief at such a crucial point in my life.
Yet another experience for abuse was with a seasoned psychiatrist who is known for his connections with Pakistan army. When army dictator Pervaiz Musharraf ruled the country, he made this doctor the dean(president) of the university of health sciences which regulates most medical universities in Pakistan. He had treated me for three years in year 2001. He started my treatment without interviewing me and gave me electric shocks at the start to jumpstart the therapy. I was given electric shocks for fifteen days in early 2001. I still recall that doctor would place a wooden wedge between my teeth and then give me an injection and I still recall how numbness would move in my body from feet to the upper body after the injection.
When going to that doctor's psychiatrist facility in 2001 I had to travel from Kot Addu to Rawalpindi. My family had given me some drug in my food and I became unconscious after an hour or so. I still recall how I was begging my younger brother to help me that I do not want to go anywhere and if he could help me but he like everybody else in the family refused. Slowly drug in food showed its effect and I have absolutely no memory of being taken in my father's car despite that it would have taken him at least eight hours to take me to Rawalpindi. Psychiatrist did not interview me and detained me and started giving me electric shocks. I still recall how I defecated in my bed there and they had to wash it.
Anyway, I was taken to this psychiatrist in 2017 again. He was very clearly told that I had been given antipsychotic drug larjactil by another doctor and it backfired and I had extremely severe drug-induced jaundice. But the doctor was so haughty and cavalier and so desperate to retard me that he still insisted that I must get the same drug larjactil and said that it was not necessary that it would cause jaundice every time. Problem for the doctor was that most antipsychotics had failed to retard me and he wanted to give me some potent antipsychotic that had not been well-tried on me. Though the drug was given to me earlier and later discontinued, the doctor wanted to take his chances to retard me and he had no regard for my health. This doctor is a big crony of Pakistan army and really wanted to please the generals and therefore he decided to give me larjactil again. And as would already be obvious to most friends, after two weeks, I started to show all signs of drug-induced jaundice again and my body and eyes were all yellow. My Biluribin shot like anything. And it took more than two months to control jaundice after that. Though my biluribin came back to normal after two months, several less known enzymes in my liver remained disturbed for several years after that and continued to show as abnormal in my liver function test reports.
I have been detained more than 30 times by various psychiatrists during past twenty-five years on orders of Pakistan Army. This is despite that I have never been violent all my life. I have never hit anyone in my adult life and I rarely speak with anyone in a loud voice. I have never done anything like breaking a glass or any utensils that is associated with sick people.
Here, I will recall an incident eight years ago when I myself approached a lady psychiatrist for help and how she abused me, and her staff beat me for twenty minutes and then tied me and started my treatment with antipsychotics again.
I am recalling this from early 2015. They had previously put me on extremely high antipsychotics and my creativity was all gone. I could barely do any intellectual work. At that time, I was able to convince my family to decrease the injections and they had agreed since I had already lost most of my creativity and intellectual capability. I think mind control agencies were also thinking that I had lost my creativity forever and they wanted to see if it was right time to decrease my drugs and still make sure that I would remain intellectually dull after injections had ended.
But I slowly started to work on my research and started to regain my brain. When mind control agencies realized that I had started to do better research, they asked my family to do something again to retard me. My father asked a self-stylized religious saint to come to our house and take care of me. He came to our house with one of his followers and told me that he wanted to give me injections and I would go to sleep for 24 hours, and they would take scans of my brain to treat me, but I continued to beg and plead him, and I was able to convince him to allow me to leave the home in my car. The supposed saint allowed me to leave since he was probably sure that he would get me later as I had no other place to go other than my home and, therefore, I was able to convince him to let me go outside. When I left the house, I made posts about the saint on at least two different forums from outside my house and pleaded for help. Enough people were following my story even at that time and the saint had to leave. I also called my father when I was outside and protested against this.
My family still remained very tense with me, and I was very afraid that they would force antipsychotics injections and mind control drugs on me therefore I stayed one night out of the home. Here is the post I made when I was away on April 14th, 2015, 2:09 pm
viewtopic.php?f=15&t=94796&start=315#p748191
"I am staying out of my home for the night since I had realized that my father will try to force me into detention again and I would request a court tomorrow for stay order to stop my father from hospitalizing me forcefully again and I would request the court that if there has to be a check on my mental health, it has to be done and investigated properly by a psychiatrist of my choice and I should remain free at the same time. I do not want to be at the mercy of my father's chosen psychiatrist as we saw in the past year that they continued to quote mental health laws and forcefully manipulate me into taking injections. If my father forcefully hospitalized me, I would be cutoff from the outer world and they would do whatever they like. My father's self-stylized saint(peer) had already hinted that he wanted to give me injections that would put me to sleep for 24 hours and he had no argument for my mental sickness at all.”
Next day, on April 15, 2015, I went to Lahore High Court to find some help but I was told that I had to submit an application that would be considered several weeks later when its turn would arrive. When I realized that there was no possibility of help from the court, I decided to see a psychiatrist on my own. I was driving in Garden town Lahore where I came across B**** psychiatric clinic and decided to see the psychiatrist Dr. N*** there. It was evening but the psychiatrist still not had arrived there. I waited for an hour in the reception and then had a consultation with her. I asked her to listen to my case carefully and then decide if I was sane enough and tell my parents about it. She said that I seemed perfectly fine and asked me that she wanted to hear what my family had to say. I agreed and took an appointment to visit her again at April 20, 2015. I took my mother on the planned day and my mother did not have anything decisive to say about any disease other than that I did not eat at home. The psychiatrist asked me to visit her after one week on 27 April 2015. The next week when I went again to visit the psychiatrist, on April 27, and was sitting in the waiting room so that I could visit the psychiatrist on my turn. Another lady who was a psychologist came to me and asked me to go with her in a different room to have a session with psychologist but I declined and said that I was only interested in seeing the psychiatrist who had promised to see me again the earlier week. After five minutes, at least four men came to the room and started besting me. They gave me slaps on my face with full force and gave me blows and they continued to do it for more than fifteen minutes. I had never been beaten like that ever before in my life. All this time, I was simply trying to raise my hand to somehow protect me. Since I was sitting on the sofa, only my face and head were the target of slaps and blows. They were very violent with all sort of slaps and blows on my face as I earlier mentioned that I was sitting and they were standing. . They literally continued to beat me and I continued to beg them to stop. After fifteen minutes of beating me, they tied my legs and lifted me and put me on a bed in a room in the psychiatrist facility and told me that doctor had gone to America and she could not see me. It was a complete lie and the psychiatrist was in her office and was interviewing other patients when I arrived. I continued to ask them to loosen the knots but they continued to make fun of me. I was totally surprised since Dr. N had behaved very nicely in the previous meeting held at 20th with my mother and myself and I was sure she would declare me mentally sane on this meeting. After I was kept tied for about half an hour, a new guard came and opened my hands and legs and said that they would keep me at the facility for three days. The next day my medication in the form of pills started and I was also given two more injections. I was given about nine pills at night and about eight pills in the morning. I was still not given the opportunity to meet the psychiatrist N, and I was told several different things by different people including that psychiatrist N had gone to America, and she had gone to Islamabad. About three days into my treatment, I saw through the glass walls that psychiatrist N was interviewing her clients in her office. After seven days, I was asked to meet psychiatrist N, and she said that she was unaware of the beating as she was in a meeting. Psychiatrist N also assured me that I had no schizophrenia and previous doctors had very wrongly diagnosed me but it was a case of some mania that she would properly treat this time. Her staff continued to say that they were giving me drugs so that the effect of other drugs given to me by previous psychiatrists would decrease.
Before my computer was taken away from me, I was able to take notes for two days in the hospital on my computer that I write here. After first two days of medication, I was so extremely weak that I could barely walk and I had extreme difficulty speaking.
“My Diary for past two days.
4/27/2015
I had two sessions with the doctor N previously on the 20th of April and once before at 13 or 14th of April. I remained away from home during this time and second meeting on 20th of April, evening after the night when I remained away from home. I had told the doctor about my circumstances in the first meeting with her. She had said that I looked perfectly fine mentally but she needed to talk to my family. On 20th of April, I took my mother for a second joint session of myself and my and the psychiatrist said, after the meeting, that said she really could not call me schizophrenic but she needed one more sessions and asked me to come to her facility on 27th of April.
When I arrived at the psychiatric facility, a psychologist had asked me to accompany her which I did and on the way to the her room, I asked for the reason, after which she replied that she wanted to take a session of mine. I told her that I already had a session with another psyc hologist and also with a psychiatrist so I would prefer to have a new session with the psychiatrist now. She agreed and I returned to the waiting room. I was sitting on a sofa in the waiting room on 27th at 8:00 PM (PST) in the line to see the psychiatrist when about five guards took control of me, while I was sitting on a sofa in the waiting room to see the doctor, and gave me an injection. I was beaten and my legs and hands were very strictly tied for more than hour. Though the doctor was in her consultation room and a lot of people were waiting to see her, I was told again and again that doctor was not present at the facility.
In the previous two sessions, she had given the impression I was healthy mentally but she used force without interviewing for the third time or seeing me and without requests to comply. If she was given any special information, she should have talked to me about it and she should have verified with me any change in circumstances.
One injection was given around 8 PM when I arrived for third session with the doctor N. I really think that the doctor was there since there was a large rush of visitors and her SUV was parked in the hospital but everybody among the staff continued to say that doctor did not come to the facility this evening.
I was kept tied for more than one hour. I was taken tied from the waiting room to my room. All these rooms have video cameras so you can ask Dr. N for a video of the events though she might make the excuse that cameras were not working. One of the staff had mentioned when they brought me into a patient room in the facility, that everything was watched by cameras.I would request people familiar with the matter to request her to show them footage of the cameras. Of course, there could be many excuses that cameras were not working but I insist that cameras were working.
Good Mental health facilities try to avoid treating humans like this.
Another injection was given at night before I slept.
and my internet USB device was also taken. They simply took possession of everything out of my pockets and also took my laptop.
When I asked why they gave me injections, one of the staff told me you were ?hyper? and I was totally surprised since I was quietly sitting on the sofa in the waiting lounge for the doctor. I was told that I would stay in the hospital for three days. I am sure this matter can be resolved who is lying and who is truthful once you look apt video footage of cameras in most rooms.
4/28/2015
One injection was given in the morning. One injection was given around noon. All injections were IM (given in the muscle.)
Unknown pills(some pills in the morning +5 pills around noon + 3 pills at night) were given and I was told,? We will tell you know the names of these pills only when you leave.?
Computer was returned today but I was told that we did not take your mobile and they continued to say we never took my mobile. My mobile was never returned( despite I always keep my mobile on me.)
I was also not given my EVO USB device and I was told you cannot write anything on internet. However the USB device was returned to my mother at night.
I was told today by the psychologist that doctor N had gone to America and will come back after seven days and only then she would be able to see you. I was told we are adjusting your medicine and see what was a good medicine. I was told they were discussing the drugs with her on phone and skype There were several conflicting statements about where Dr. N was. Somebody said she was just out of city and had gone to Islamabad.
When I asked my mother who is living with me at the hospital, I wanted a second opinion, because of beating and other irresponsible behavior of the psychiatrist, my mother would make all sort of excuses while the staff would say that you cannot leave the hospital until Dr. N arrives who is currently out of country.
Earlier today, I was told that I would live at the hospital for fifteen days and later I was told that I would live at the facility for seven days. When I was tied, somebody had told me that I would live in the hospital for three days only.
My mother told me please do not write anything wrong on internet otherwise, they would take your USB forcefully like Dr. A had done more than one year ago. The purpose was to threaten me to not write about any maltreatment so that the doctor would continue to freely manipulate me.
7-8 pills were given in the afternoon and similar number of pills were given at night. At many times during the day, I could barely walk and had extreme difficulty speaking.”
The excerpt below is from a past post stating obvious abuse by various psychiatrists on the insistence of mind control agencies. The episode of physical abuse by beating me for more than twenty minutes is towards the end of this post:
Friends, I wanted to remain busy with my research and not speak about mind control and its reasons and people behind it. I simply wanted to concentrate on my research but whenever I have any progress in my research, my mind control and related torture sharply increases to make more research impossible for me. I want to remain totally devoted to my research and want friends to help me in doing that, I want everyone of all the good people in Europe or America who follow my research to please tell two or three journalists about my research and my mind control. I will also request European friends to ask their government and embassies to please keep a vigil about the matter and force corrupt Pakistani govt. and establishment to not drug food in Lahore with mind control chemicals.
I was a very simple, very meek but also very hard working student at a large university in New York and joined the university in 1997. My mind control started in very late 1997 when a racist jewish professor in Math department of my university was threatened by my talent and approached the Jewish Billionaire to ask American defense to put me under mind control. Even that long time ago, a large number of jews were very aware that this Jewish billionaire was a Godfather of mind control and would approach the billionaire to recommend talented people to mind control from time to time when they would be threatened by their talent. Over past twenty five years tens of thousands (if not more than a hundred thousand) of innocent people mostly American nationals have been placed on mind control abuse by scumbags of American defense on recommendation of Jewish billionaire. Most universities in US have a couple of jews who continue to keep eye on brilliant students of the university and recommend them to American defense through jewish billionaire when they feel threatened by the talent of the students due to any reason like their religion, race, ethnicity or just because they are not jews.
I had told friends earlier that a jewish billionaire is Godfather of mind control. When my persecution started (in late 1997) at the university in New York which is a big time player in mind control of Muslims, blacks and foreigners, many university officials were very pleased that they were getting written in good books of the billionaire jewish Godfather. Though there are far richer billionaires in US who are staunchly opposed to mind control, they are not ready to shell out hundreds of millions of dollars to bribe anyone to end mind control while mind control Godfather continues to give large bribes to people to continue mind control. Many of the people related to defense in mind control are given extremely high paying jobs in Godfather and his other jewish friends' companies after they retire from mind control and Godfather is extremely generous towards them and it is well established and well known to scum in mind control that after retarding muslims, blacks and others in their career, they will move to paradise(tens of people from army/Pentagon who follow whims of Billionaire Godfather are given jobs paying milllons of dollars by Godfather and his jewish cohort in several companies) after they retire. No wonder there is no let up in mind control whatever good people try.
We know in almost all classic folk lore stories evil is too strong and too sure of itself while good is mostly weak and just trying to protect itself from evil who is bent on damaging and eradicating the weak and the poor good but it is the weak and poor good that finally prevails. I want to tell good American friends that evil at this stage has become too bold and thousands of talented people are retarded every year. And it is just not muslims and blacks that are on the line, several thousands of brilliant whites are retarded across United States by mind control agency every year that has become too emboldened due to lack of any accountability. Thousands of foreigners are also kept retarded in dozens of countries including many European countries.
My only intention behind this post is that I want mind control to end from our societies. I do not have any joy in mentioning that there are some bad jewish actors behind it. In American society there are a large number of jews who have excelled in the professions of science, education, medicine and have made great contributions to our societies. There are a very large number of jewish professors each of whom would have taught tens of thousands of students on top of making extraordinary contributions to body of human knowledge through their great research. Then there are accomplished jewish scientists whose work, research and inventions make our everyday life better. There are great jewish doctors and surgeons who would treat countless sick people and make them recover from disease. The list of contributions of jewish people to humanity is very long and it continues. Then there are a large number of ordinary jewish folks who are known for their goodness and civility to other people in the society. When we know all of this, we do not want to say anything anti-jewish to hurt the feelings of so many good jewish people. But I still have to say there are really some bad people who are unconnected with most of the nice and accomplished jews and they instigate and continue cruel mind control torture on talented people of other ethnicities, religions and countries based on their personal dislike and hatred. My purpose is only to end the mind control victimization and torture on otherwise nice and talented people and I do not have any hidden intentions beyond that. And I am sure American society knows very well about the contributions of good Jews to both their country and broader humanity and my exposing some bad actors would never have any bad effect of any kind on these good and nice jews who we all respect and who are our role models.I want to tell friends something I have said before here that I am sure American society would eventually end the menace of mind control from their and other countries. I want to request all good Americans and Europeans to come forward and invite any investigative journalist you know to read my threads and ask them to help end the menace of mind control in our societies through their investigative journalism. Without any accountability evil will continue to grow stronger and then mind control would start to threaten even those people who consider themselves safe due to affiliations, status or wealth.
https://forum.wilmott.com/viewtopic.php?t=99702&start=2325#p881807
https://forum.wilmott.com/viewtopic.php?t=99702&start=2325#p881808
https://forum.wilmott.com/viewtopic.php?t=99702&start=2325#p881886
https://forum.wilmott.com/viewtopic.php?t=99702&start=2340#p881951
Friends, this speaks volumes about headstrong cruelty of people in American defense and their Jewish billionaire backers cohort that they are even more ready to show me cruelties even after people have a widespread knowledge of their machinations and tactics. These evil people have no intention or desire to decrease their torture on me despite that I have been telling tales of their inhuman torture on me over past twenty five years through various psychiatrists.
Please read the following two posts to see the context how I have been maltreated by various psychiatrists on behest of mind control agencies over past 25 years.
Friends, I have been on forced antipsychotics for most of the time since early 1999. There were a few periods of a few months when I remained free from antipsychotics. But other than two or three such periods, I have remained on antipsychotics. It is very hard to feel well when huge antipsychotics are forced on someone who is mentally healthy. I have also been detained forcefully tens of times whenever some of my neurotransmitters came back, the purpose of detention was to take brilliant neurotransmitters out of my brain and send me back home with a relatively retarded brain after the end of months long detentions. I have seen sheer trauma, torture and brutality on the hands of these psychiatrists who connive with American defense and Pakistani military to declare me mentally ill so they can force antipsychotics on me. I will be 51 this year and portion of my life that I lived under mind control has exceeded the part of early life that I lived without mind control.
I have a phone meeting with the psychiatrist on 14th of June 2024. And I am sure the psychiatrist will try again to keep me under medication or even increase my medication. Even after a large number of people have become aware of truth about mind control and accompanying persecution by the psychiatrists, most psychiatrists are not the least worried that their wrongdoing is being exposed in public.
I want to request good Americans to please protest to American defense, mind control agency, Pak army and relevant psychiatrists to please end this cruel practice of declaring healthy people on antipsychotics and forcefully detaining them up to years in their faciiities.
When they detain me, they have fixed all mind control gadgets and lasers in the psychiatric facility and they add all mind control chemicals openly in food and psychiatric drugs. It is a very controlled environment in captivity and within a month or so, they are able to remove all neurotransmitters from the brain of the victim. Every time I was detained, they kept me in the psychiatric facility for 30-50 days. One psychiatric even detained me for ten months after I returned from Britain. There are also instances of being detained for six months once and three months twice.
I really want to request American people again to please protest to their government and try to make sure that I am not being detained again on totally flimsy psychiatric grounds.
.
My Letter To HRW About My Human Rights Abuse
Above is a very incomplete account of how various psychiatrists continued to play in hands of Pakistan army to retard me. It also does not cover all the time till year 2022 and the account stops several years earlier. I could not write about last several years that were exceptionally brutal.
Friends, in a previous post I told friends how staff at a lady psychiatrist's hospital started beating me and abused me. During past twenty three years, there have been many many instances of my obvious abuse by different psychiatrists. I will describe some of those instances in this post.
When I came from United States and till fifteen years after that, my father would proudly ask me that I could see any psychiatrist I wish. This was because Pakistan army was managing my persecution and they would force psychiatrists to declare me schizophrenic and my father was told that every psychiatrist would be forced to cooperate. However, by chance in 2016, I came across a psychiatrist who was far better. I never told him that I was under mind control but whenever he interviewed me, he always said after the interview that I was perfectly sane and mentally healthy. When my family would force him to increase the dosage of antipsychotics, the doctor first told me that I should not live with my family and make a comprehensive plan to support myself and become independent (such a plan could never work since Pakistan army was threatening people in Pakistan to not give me any business and CIA was making sure that every contact I would reach for work in Europe (and Singapore/ Japan /Australia) would be approached by CIA telling them that I was a very bad guy and they must not do business with me. I had not told the doctor any such thing that intelligence agencies were after me.) When I told the good doctor how previous psychiatrists had abused me, he would tell me that this used to be a very widespread practice in America hundred years ago to wrong mentally healthy humans by using corrupt psychiatrists as instruments to detain them and strip them of their sanity. The good doctor I am talking about was American national with Pakistan background who had practiced psychiatry in America for over twenty years and had returned to Pakistan. That good doctor kept me on very low antipsychotics (1 mg resperidone per day) and that too on extreme insistence of my family. It was only during that time of treatment by that doctor that I got my first break in research and I solved the problem of high order monte carlo simulations (and analytic series solution of ODEs) and posted that solution on this thread. Ok, when my family was fed with the doctor, they detained me with another doctor. They detained me again two years ago when I requested my family that I wanted to see the same doctor of my choice again( I have been detained every year for past six or seven years by different doctors), they detained me through a different doctor. So my family now stubbornly refuses to allow me to see a professional qualified American psychiatrist of my own choice and detains me every time I try to approach him.
Now back to my obvious abuse by two other psychiatrists. I was detained by this doctor who was running a mental health facility and was not a psychiatrist himself. At that time I did not use to walk very much and my blood pressure used to be somewhat high. Since other antipsychotics had failed to retard me, doctor suggested I take aripperizole injections. These injections affect the heart and also elevate blood pressure but doctor who wanted to retard me had no regard for my health while pretending to cure me. In initial days of my detention, staff at the hospital when checked my blood pressure told me high enough blood pressure in line with what I used to have but after I complained about aripperizole and its effect on blood pressure the staff started doctoring blood pressure and started telling me that my blood pressure was very good or even low. This is a post I wrote on another thread in this forum about it. How to safeguard my research - Page 32 - wilmott.com
.
.Amin:
Since I wrote about high blood pressure and mentioned high blood pressure before the hospital staff, they have started to doctor blood pressure. Now, everyday they tell me that my blood pressure is 120/80 or 110/70. While they always told me that my blood pressure was 130/90 or 140/100 prior to injections. I have never had so good blood pressure for years that they have started to tell me now. Friends would recall a previous post when I could not sleep at night and had to take a sleeping pill. When the dispenser came to me at night(The hospital has no MBBS who stays here at night in Ramadan. Dr. AS used to stay here on some nights earlier but has been totally absent in Ramadan). When the dispenser checked my blood pressure, he told me that it upper blood pressure is 110. I did not believe him at all. He asked me to check on my own and put the stethoscope head assembly in my ears. I could easily tell that upper blood pressure was more than 140 and lower was more than 100. The staff has already started to doctor blood pressure. My parents are going to Saudi Arabia for two weeks in a few days. Now Dr. AS has the plan to hold me in detention while my parents are abroad. I had a complete settlement with Dr. N and we(I and the doctor N) both agreed that I would be visiting him every fifteen days and all modalities were agreed. I do think as a patient it is my right to choose the psychiatrist and Dr. AS( who is incharge of facility Pav.) has no right to change the doctor after I have selected a psychiatrist and we both agree on terms of any treatment. Dr. AS has imposed another psychiatrist Dr. M who has not even seen me and has already started giving me injections and increased medicine without looking at my present condition. Dr. N had explicitly stated that I would be free to leave if it were his facility. Most major reason for detaining me now is that Dr.AS wants to continue to detain me while my parents are leaving for abroad for more than two weeks
Later after a few days, I was given a second aripperizole injection and released from detention. An injection was due every fifteen days. My parents were in Saudi Arabia and I was living with my sister. She insisted after fifteen days that I get a new aripperizole injection. I complained about too much side effects and other serious problems but my sister insisted that I must get the injection. She talked to another doctor and the doctor told her that if his blood pressure and pulse are fine, just give him the injection. I asked my sister that my blood pressure must be checked before I get the new injection. We went to a small hospital close to her house and when my blood pressure was checked my lower blood pressure was 110. The hospital staff recommended that I stay at the hospital in their care until my blood pressure decreases. It was a totally random blood perssure check. When hospital staff came to know that I had been given aripperizole injections, they told my sister to not give me those injections any more. My sister asked the staff to relieve me and we came home but I was not given aripperizole injections after that.
But this is interesting that the psychiatrist was initially desperate to prescribe aripperizole despite that I had told him about my heart and blood pressure problems and his staff was asked to doctor blood pressure so that I would accept the injections.
Good thing is that only after stopping aripperizole, I started my treatment with good psychiatrist doctor Naeem Aftab (who is an American national) and he gave me enough relief that I was able to get a break in my research and solve the problem of high order monte carlo simulations. I would always be thankful to Dr. Naeem Aftab for giving me relief at such a crucial point in my life.
Yet another experience for abuse was with a seasoned psychiatrist who is known for his connections with Pakistan army. When army dictator Pervaiz Musharraf ruled the country, he made this doctor the dean(president) of the university of health sciences which regulates most medical universities in Pakistan. He had treated me for three years in year 2001. He started my treatment without interviewing me and gave me electric shocks at the start to jumpstart the therapy. I was given electric shocks for fifteen days in early 2001. I still recall that doctor would place a wooden wedge between my teeth and then give me an injection and I still recall how numbness would move in my body from feet to the upper body after the injection.
When going to that doctor's psychiatrist facility in 2001 I had to travel from Kot Addu to Rawalpindi. My family had given me some drug in my food and I became unconscious after an hour or so. I still recall how I was begging my younger brother to help me that I do not want to go anywhere and if he could help me but he like everybody else in the family refused. Slowly drug in food showed its effect and I have absolutely no memory of being taken in my father's car despite that it would have taken him at least eight hours to take me to Rawalpindi. Psychiatrist did not interview me and detained me and started giving me electric shocks. I still recall how I defecated in my bed there and they had to wash it.
Anyway, I was taken to this psychiatrist in 2017 again. He was very clearly told that I had been given antipsychotic drug larjactil by another doctor and it backfired and I had extremely severe drug-induced jaundice. But the doctor was so haughty and cavalier and so desperate to retard me that he still insisted that I must get the same drug larjactil and said that it was not necessary that it would cause jaundice every time. Problem for the doctor was that most antipsychotics had failed to retard me and he wanted to give me some potent antipsychotic that had not been well-tried on me. Though the drug was given to me earlier and later discontinued, the doctor wanted to take his chances to retard me and he had no regard for my health. This doctor is a big crony of Pakistan army and really wanted to please the generals and therefore he decided to give me larjactil again. And as would already be obvious to most friends, after two weeks, I started to show all signs of drug-induced jaundice again and my body and eyes were all yellow. My Biluribin shot like anything. And it took more than two months to control jaundice after that. Though my biluribin came back to normal after two months, several less known enzymes in my liver remained disturbed for several years after that and continued to show as abnormal in my liver function test reports.
I have been detained more than 30 times by various psychiatrists during past twenty-five years on orders of Pakistan Army. This is despite that I have never been violent all my life. I have never hit anyone in my adult life and I rarely speak with anyone in a loud voice. I have never done anything like breaking a glass or any utensils that is associated with sick people.
Here, I will recall an incident eight years ago when I myself approached a lady psychiatrist for help and how she abused me, and her staff beat me for twenty minutes and then tied me and started my treatment with antipsychotics again.
I am recalling this from early 2015. They had previously put me on extremely high antipsychotics and my creativity was all gone. I could barely do any intellectual work. At that time, I was able to convince my family to decrease the injections and they had agreed since I had already lost most of my creativity and intellectual capability. I think mind control agencies were also thinking that I had lost my creativity forever and they wanted to see if it was right time to decrease my drugs and still make sure that I would remain intellectually dull after injections had ended.
But I slowly started to work on my research and started to regain my brain. When mind control agencies realized that I had started to do better research, they asked my family to do something again to retard me. My father asked a self-stylized religious saint to come to our house and take care of me. He came to our house with one of his followers and told me that he wanted to give me injections and I would go to sleep for 24 hours, and they would take scans of my brain to treat me, but I continued to beg and plead him, and I was able to convince him to allow me to leave the home in my car. The supposed saint allowed me to leave since he was probably sure that he would get me later as I had no other place to go other than my home and, therefore, I was able to convince him to let me go outside. When I left the house, I made posts about the saint on at least two different forums from outside my house and pleaded for help. Enough people were following my story even at that time and the saint had to leave. I also called my father when I was outside and protested against this.
My family still remained very tense with me, and I was very afraid that they would force antipsychotics injections and mind control drugs on me therefore I stayed one night out of the home. Here is the post I made when I was away on April 14th, 2015, 2:09 pm
viewtopic.php?f=15&t=94796&start=315#p748191
"I am staying out of my home for the night since I had realized that my father will try to force me into detention again and I would request a court tomorrow for stay order to stop my father from hospitalizing me forcefully again and I would request the court that if there has to be a check on my mental health, it has to be done and investigated properly by a psychiatrist of my choice and I should remain free at the same time. I do not want to be at the mercy of my father's chosen psychiatrist as we saw in the past year that they continued to quote mental health laws and forcefully manipulate me into taking injections. If my father forcefully hospitalized me, I would be cutoff from the outer world and they would do whatever they like. My father's self-stylized saint(peer) had already hinted that he wanted to give me injections that would put me to sleep for 24 hours and he had no argument for my mental sickness at all.”
Next day, on April 15, 2015, I went to Lahore High Court to find some help but I was told that I had to submit an application that would be considered several weeks later when its turn would arrive. When I realized that there was no possibility of help from the court, I decided to see a psychiatrist on my own. I was driving in Garden town Lahore where I came across B**** psychiatric clinic and decided to see the psychiatrist Dr. N*** there. It was evening but the psychiatrist still not had arrived there. I waited for an hour in the reception and then had a consultation with her. I asked her to listen to my case carefully and then decide if I was sane enough and tell my parents about it. She said that I seemed perfectly fine and asked me that she wanted to hear what my family had to say. I agreed and took an appointment to visit her again at April 20, 2015. I took my mother on the planned day and my mother did not have anything decisive to say about any disease other than that I did not eat at home. The psychiatrist asked me to visit her after one week on 27 April 2015. The next week when I went again to visit the psychiatrist, on April 27, and was sitting in the waiting room so that I could visit the psychiatrist on my turn. Another lady who was a psychologist came to me and asked me to go with her in a different room to have a session with psychologist but I declined and said that I was only interested in seeing the psychiatrist who had promised to see me again the earlier week. After five minutes, at least four men came to the room and started besting me. They gave me slaps on my face with full force and gave me blows and they continued to do it for more than fifteen minutes. I had never been beaten like that ever before in my life. All this time, I was simply trying to raise my hand to somehow protect me. Since I was sitting on the sofa, only my face and head were the target of slaps and blows. They were very violent with all sort of slaps and blows on my face as I earlier mentioned that I was sitting and they were standing. . They literally continued to beat me and I continued to beg them to stop. After fifteen minutes of beating me, they tied my legs and lifted me and put me on a bed in a room in the psychiatrist facility and told me that doctor had gone to America and she could not see me. It was a complete lie and the psychiatrist was in her office and was interviewing other patients when I arrived. I continued to ask them to loosen the knots but they continued to make fun of me. I was totally surprised since Dr. N had behaved very nicely in the previous meeting held at 20th with my mother and myself and I was sure she would declare me mentally sane on this meeting. After I was kept tied for about half an hour, a new guard came and opened my hands and legs and said that they would keep me at the facility for three days. The next day my medication in the form of pills started and I was also given two more injections. I was given about nine pills at night and about eight pills in the morning. I was still not given the opportunity to meet the psychiatrist N, and I was told several different things by different people including that psychiatrist N had gone to America, and she had gone to Islamabad. About three days into my treatment, I saw through the glass walls that psychiatrist N was interviewing her clients in her office. After seven days, I was asked to meet psychiatrist N, and she said that she was unaware of the beating as she was in a meeting. Psychiatrist N also assured me that I had no schizophrenia and previous doctors had very wrongly diagnosed me but it was a case of some mania that she would properly treat this time. Her staff continued to say that they were giving me drugs so that the effect of other drugs given to me by previous psychiatrists would decrease.
Before my computer was taken away from me, I was able to take notes for two days in the hospital on my computer that I write here. After first two days of medication, I was so extremely weak that I could barely walk and I had extreme difficulty speaking.
“My Diary for past two days.
4/27/2015
I had two sessions with the doctor N previously on the 20th of April and once before at 13 or 14th of April. I remained away from home during this time and second meeting on 20th of April, evening after the night when I remained away from home. I had told the doctor about my circumstances in the first meeting with her. She had said that I looked perfectly fine mentally but she needed to talk to my family. On 20th of April, I took my mother for a second joint session of myself and my and the psychiatrist said, after the meeting, that said she really could not call me schizophrenic but she needed one more sessions and asked me to come to her facility on 27th of April.
When I arrived at the psychiatric facility, a psychologist had asked me to accompany her which I did and on the way to the her room, I asked for the reason, after which she replied that she wanted to take a session of mine. I told her that I already had a session with another psyc hologist and also with a psychiatrist so I would prefer to have a new session with the psychiatrist now. She agreed and I returned to the waiting room. I was sitting on a sofa in the waiting room on 27th at 8:00 PM (PST) in the line to see the psychiatrist when about five guards took control of me, while I was sitting on a sofa in the waiting room to see the doctor, and gave me an injection. I was beaten and my legs and hands were very strictly tied for more than hour. Though the doctor was in her consultation room and a lot of people were waiting to see her, I was told again and again that doctor was not present at the facility.
In the previous two sessions, she had given the impression I was healthy mentally but she used force without interviewing for the third time or seeing me and without requests to comply. If she was given any special information, she should have talked to me about it and she should have verified with me any change in circumstances.
One injection was given around 8 PM when I arrived for third session with the doctor N. I really think that the doctor was there since there was a large rush of visitors and her SUV was parked in the hospital but everybody among the staff continued to say that doctor did not come to the facility this evening.
I was kept tied for more than one hour. I was taken tied from the waiting room to my room. All these rooms have video cameras so you can ask Dr. N for a video of the events though she might make the excuse that cameras were not working. One of the staff had mentioned when they brought me into a patient room in the facility, that everything was watched by cameras.I would request people familiar with the matter to request her to show them footage of the cameras. Of course, there could be many excuses that cameras were not working but I insist that cameras were working.
Good Mental health facilities try to avoid treating humans like this.
Another injection was given at night before I slept.
and my internet USB device was also taken. They simply took possession of everything out of my pockets and also took my laptop.
When I asked why they gave me injections, one of the staff told me you were ?hyper? and I was totally surprised since I was quietly sitting on the sofa in the waiting lounge for the doctor. I was told that I would stay in the hospital for three days. I am sure this matter can be resolved who is lying and who is truthful once you look apt video footage of cameras in most rooms.
4/28/2015
One injection was given in the morning. One injection was given around noon. All injections were IM (given in the muscle.)
Unknown pills(some pills in the morning +5 pills around noon + 3 pills at night) were given and I was told,? We will tell you know the names of these pills only when you leave.?
Computer was returned today but I was told that we did not take your mobile and they continued to say we never took my mobile. My mobile was never returned( despite I always keep my mobile on me.)
I was also not given my EVO USB device and I was told you cannot write anything on internet. However the USB device was returned to my mother at night.
I was told today by the psychologist that doctor N had gone to America and will come back after seven days and only then she would be able to see you. I was told we are adjusting your medicine and see what was a good medicine. I was told they were discussing the drugs with her on phone and skype There were several conflicting statements about where Dr. N was. Somebody said she was just out of city and had gone to Islamabad.
When I asked my mother who is living with me at the hospital, I wanted a second opinion, because of beating and other irresponsible behavior of the psychiatrist, my mother would make all sort of excuses while the staff would say that you cannot leave the hospital until Dr. N arrives who is currently out of country.
Earlier today, I was told that I would live at the hospital for fifteen days and later I was told that I would live at the facility for seven days. When I was tied, somebody had told me that I would live in the hospital for three days only.
My mother told me please do not write anything wrong on internet otherwise, they would take your USB forcefully like Dr. A had done more than one year ago. The purpose was to threaten me to not write about any maltreatment so that the doctor would continue to freely manipulate me.
7-8 pills were given in the afternoon and similar number of pills were given at night. At many times during the day, I could barely walk and had extreme difficulty speaking.”
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I take fenugreeks seeds, carom seeds/bishop's weed and cinnamon in my tea almost twice everyday. Fenugreek seeds increase metabolism. I am kept sedated all the time by antipsychotic injections and have low metabolism. I also have hypo-thyroidism in which metabolism decreases.
Mind control agents do not like my taking any herbs in my key since they are good for my body. Now they have drugged fenugreek seeds on a huge scale with mind control drugs. I think they mix drugs in fenugreek seeds in the market where all the whole sale dealers of food in the Lahore are located. I bought fenugreek seeds from a totally random store and it was a store chain that had packed fenugreek seeds for themselves and no vendors had supplied the seeds. However the packing date on seeds was recent probably 18th August 2025. I am sure they are adding drugs in fenugreeks seeds in the wholesale market of Lahore city.
Friends, these mind control people are so anal and and so malicious, they would add drugs to underground water in the whole city but if I switch to Pepsi-Cola or Coca-Cola, they keep them undrugged because these beverages are so unhealthy for me but they would not let me drink good water as this is the most healthy drink. Any healthy food or herb I take, they want to stop me from taking it. Here I recall that I had liver problems (that I still have) and they drugged a lot of liver tonics and hepa-merz (which is a universal drug to make liver better) with mind control drugs so that I cannot take it.
I had run out of fenugreek seeds and bought them again today and when I had taken just very small sip, my mind was completely altered and I am still reeling from that effect. I had several ideas about my work but I cannot do any work and kept ranting for almost half an hour a little earlier. And therefore I made the previous post as well since water in the city is getting drugged cruelly again and they are drugging other things as well. Please stop these anal heroes of mind control from showing their cruelty to good human beings. I beg good people to please stop these cruel people from their open cruelties.
Mind control agents do not like my taking any herbs in my key since they are good for my body. Now they have drugged fenugreek seeds on a huge scale with mind control drugs. I think they mix drugs in fenugreek seeds in the market where all the whole sale dealers of food in the Lahore are located. I bought fenugreek seeds from a totally random store and it was a store chain that had packed fenugreek seeds for themselves and no vendors had supplied the seeds. However the packing date on seeds was recent probably 18th August 2025. I am sure they are adding drugs in fenugreeks seeds in the wholesale market of Lahore city.
Friends, these mind control people are so anal and and so malicious, they would add drugs to underground water in the whole city but if I switch to Pepsi-Cola or Coca-Cola, they keep them undrugged because these beverages are so unhealthy for me but they would not let me drink good water as this is the most healthy drink. Any healthy food or herb I take, they want to stop me from taking it. Here I recall that I had liver problems (that I still have) and they drugged a lot of liver tonics and hepa-merz (which is a universal drug to make liver better) with mind control drugs so that I cannot take it.
I had run out of fenugreek seeds and bought them again today and when I had taken just very small sip, my mind was completely altered and I am still reeling from that effect. I had several ideas about my work but I cannot do any work and kept ranting for almost half an hour a little earlier. And therefore I made the previous post as well since water in the city is getting drugged cruelly again and they are drugging other things as well. Please stop these anal heroes of mind control from showing their cruelty to good human beings. I beg good people to please stop these cruel people from their open cruelties.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, mind control guy continues to say that they will be better if I start working with one of their chosen guys. I do not mean to be offensive to anyone and there are many very accomplished people in probability theory (probably they are never the ones mind control guy wants me to work for) and some very respected and accomplished Jews in probability theory who are also very good human beings. But I have absolutely no way to know who is genuine with me. Besides mind control guy wants me to work for someone solely so that I would not be able to share my work freely after that. I believe in sharing my work freely since I have always believed that any advances in science when they are accessible to everyone is an absolutely good thing. If humans have been able to build a formidable civilization, it all due to so many good scientists, mathematicians and engineers who were able to advance science. Please let us all walk in the footstep of humanity that made good things possible for all of us. It is the worst form of racism when a Jew says that a Muslim would not be allowed to do any research and share this research with others because Muslims are not supposed(or allowed) to do so. I am sure many people understand the meanings of this racism. Please let us all try to have good ideals and let us all try to do something good and positive in this world.
Besides, I have been able to find my way out of religion as I oriented myself (by studying about) in this universe and in the history of this earth and this universe. I do not believe in any religion and there are many muslims (by birth) like me who are not given the opportunity to do anything good in this world because there is a scumbag Jewish billionaire who is Godfather of mind control and he decides so. Please stop this cruelty now forever.
This is so bad but many jews remain insecure that if Muslims do good science in US and other places, the jewish control (as is evident by complete control of Jewish scumbag over US defense by the scumbag billionaire) would decrease and Israeli hostilities would no longer be tolerated. For example, I am not in any way against existence of Israel and want all Muslim countries to have good diplomatic relations with Israel and then leverage these good relationships to have enough human space for palestinians to live with enough human dignity. I am against all inhuman acts of Hamas against Israelis and totally denounce that(Just as I denounce Israeli inhuman and barbaric acts on innocent civilians.) But I do not believe in harming any jew in any way even though I openly speak against some of the bad ones on this forum. Again most of the people like me fully acknowledge the Israeli right to exist and want our nations to have full diplomatic relations with Israel and then leverage these relations to get a good enough deal for Palestinians. But this is funny how so many Jews in US become insecure when they see muslim students working hard and they a large number of these students are put on mind control. This has to end. Even though I write against bad jews who are behind the practice of Mind control, I have nothing against good jews and want to tell that most educated Muslims are not irrational about Israel at all.
Besides, I have been able to find my way out of religion as I oriented myself (by studying about) in this universe and in the history of this earth and this universe. I do not believe in any religion and there are many muslims (by birth) like me who are not given the opportunity to do anything good in this world because there is a scumbag Jewish billionaire who is Godfather of mind control and he decides so. Please stop this cruelty now forever.
This is so bad but many jews remain insecure that if Muslims do good science in US and other places, the jewish control (as is evident by complete control of Jewish scumbag over US defense by the scumbag billionaire) would decrease and Israeli hostilities would no longer be tolerated. For example, I am not in any way against existence of Israel and want all Muslim countries to have good diplomatic relations with Israel and then leverage these good relationships to have enough human space for palestinians to live with enough human dignity. I am against all inhuman acts of Hamas against Israelis and totally denounce that(Just as I denounce Israeli inhuman and barbaric acts on innocent civilians.) But I do not believe in harming any jew in any way even though I openly speak against some of the bad ones on this forum. Again most of the people like me fully acknowledge the Israeli right to exist and want our nations to have full diplomatic relations with Israel and then leverage these relations to get a good enough deal for Palestinians. But this is funny how so many Jews in US become insecure when they see muslim students working hard and they a large number of these students are put on mind control. This has to end. Even though I write against bad jews who are behind the practice of Mind control, I have nothing against good jews and want to tell that most educated Muslims are not irrational about Israel at all.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I slept earlier yesterday at 8:30 pm and did not work at night. The whole night mind control agents continue to fire microwaves on me and I had a very rough sleep. They particularly shoot microwaves in the closed sleeping eyes and my eyes become saltish due to that and I have to throw water into inside of my eyes (wash inside of my eyes with water) to be able to see properly otherwise it is painful to even open the eyes (when I have not washed them). So it was basically a rough night and I did not have a proper sound sleep at all.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, I have been trying to work with problem of getting properly tailed model densities that are faithful to their true conditional values. I noticed that any optimization should first try to fit the smaller moments better and then move on to fitting the higher moments. And then I have this idea of using various objective function criteria of fit for that purpose. I start the optimization with an objective function (that has to be minimized) that gives a very large weight to smaller moments. Then after some iterations of the optimization function, I slowly shift to objective function that places slightly less higher weight to smaller moments and relatively larger weight(as compared to in the previous objective function) to higher moments. And I continue to shift about four objective functions and finally end at the objective function that is plain sum of squared differences between cross-moments. In this way, I mostly get a properly tailed density that is quite reasonably close to the true conditional density.
Here are my various objective functions out of my matlab program.
.
.
Here weights w2D4 place a relatively very high weight on smaller moments. I start with w2D4 and after a few hundred iterations, I switch to w2D3 and continue to switch to w2D2, w2D1, w2Dh and finally w2D0.
This way optimization takes a path that does not overfit higher moments too early to cause all sort of instabilities and higher moments are slowly fitted only after smaller moments have become a good fit. I hope to post a program based on that tomorrow.
Very sorry that I had earlier mentioned that I would describe all the details of the method over past weekend but I continued to try to improve the previous work. But just in a day or two, I would post all the details with latex equations. Sorry again for this delay as some friends might be waiting for this introduction to get oriented with the method.
Here are my various objective functions out of my matlab program.
Code: Select all
w2D0(1:NMomentsY,1:NMomentsX)=1;
w2Dh(1:NMomentsY,1:NMomentsX)=1;
w2D1(1:NMomentsY,1:NMomentsX)=1;
w2D2(1:NMomentsY,1:NMomentsX)=1;
w2D3(1:NMomentsY,1:NMomentsX)=1;
w2D4(1:NMomentsY,1:NMomentsX)=1;
for nn=NMomentsY-1:-1:1
for mm=NMomentsX-1:-1:1
w2Dh(nn,mm)=w2Dh(nn+1,mm+1)*(nn+1).^.5*(mm+1).^.5;
w2D1(nn,mm)=w2D1(nn+1,mm+1)*(nn+1)*(mm+1);
w2D2(nn,mm)=w2D2(nn+1,mm+1)*(nn+1).^2*(mm+1).^2.0;
w2D3(nn,mm)=w2D3(nn+1,mm+1)*(nn+1).^3*(mm+1).^3.0;
w2D4(nn,mm)=w2D4(nn+1,mm+1)*(nn+1).^4*(mm+1).^4.0;
end
end
.
Here weights w2D4 place a relatively very high weight on smaller moments. I start with w2D4 and after a few hundred iterations, I switch to w2D3 and continue to switch to w2D2, w2D1, w2Dh and finally w2D0.
This way optimization takes a path that does not overfit higher moments too early to cause all sort of instabilities and higher moments are slowly fitted only after smaller moments have become a good fit. I hope to post a program based on that tomorrow.
Very sorry that I had earlier mentioned that I would describe all the details of the method over past weekend but I continued to try to improve the previous work. But just in a day or two, I would post all the details with latex equations. Sorry again for this delay as some friends might be waiting for this introduction to get oriented with the method.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
Re: Breakthrough in the theory of stochastic differential equations and their simulation
Friends, before I explain 2D Z-series, some basic things about 1D Z-series starting very simple for proper orientation.
What is a Z-series?
Z-series of a one dimensional continuous random variable is a power series/Taylor Series mapping of a random variable on a standard Gaussian. When we say Z-series, we refer to coefficients associated with different powers of standard Gaussian in that mapping. Z-series is not directly a density itself but has an associated density that can be found by taking a Jacobian of the random variable with respect to the standard Gaussian density on which it is mapped.
Z-Series of a random variable X is given as
\[\,X\,=\, a_0 \, +\, a_1 \,Z \,+\, a_2 \,{Z}^2 \,+\, a_3 \,{Z}^3 \,+\,\ldots\]
We store the coefficients of the above Series in an array and call these coefficients Z-series when it comes to all the programming.
We also point out that Jacobian assciated with X, and written in notation \(\frac{dX}{dZ}\) is given as
\[\,\frac{dX}{dZ}\,=\,\, a_1 \,+\,2\, a_2 \,{Z} \,+\,3\, a_3 \,{Z}^2 \,\,+\,4\, a_4 \,{Z}^3 \,+\,\ldots\]
The density of the random variable X is then found using above Jacobian as
\[\,p_X(X)\,=\,p_Z(Z(X))\,\,|\frac{dZ}{dX}|\]
Again Z-series itself is distinct from the density and not a density in itself but has an associated density that can easily be found.
Every Z-series has an associated Hermite series which is algebraically equivalent to its Z-series and when algebraically collapsed both are exactly equivalent. A Hermite series is just algebraically re-arranged so that the whole series appears as coefficients of Hermite polynomials. This is because hermite polynomials have a full span and every Nth degree polynomial can be written as coefficients of first N Hermite polynomials.
This Hermite series is given as
\[\,X\,=\, ah_0 \, +\, ah_1 \,H_1(Z_x) \,+\, ah_2 \,H_2(Z_x) \,+\, ah_3 \,H_3(Z_x) \,+\,\ldots\]
When referring Hermite series in the context of a computer program, we refer to the array storing coefficients \(ah_n\) of the Hermite Polynomials.
For friends who want to follow the programs, In the programming, I have extensively used "Order" of a Z-series. It is basically the highest power of Z in the Z-series or alternatively highest hermite-polynomial in the hermite-series. I have used another programming variable SeriesOrder but that can change with context to "Order" or to "Order+1". However "Order" always have the same meanings throughout. This will be helpful when you try to understand the programs. Usually it is natural that a hermite series with Order=N, will be fitted to N+1 moments.
I gave this very small review to univariate Z-series for context to properly orient friends and will now move in next post to 2D Z-series and its related programming. If you want to know more about univariate Z-series, please read my paper on SSRN here : Representation of Non-Gaussian Continuous Random Variables by a Taylor Series in Standard Gaussian Random Variable: Estimation, Analytics and Applications
One more thing to mention. In older programs, when I was rather naive about how to deal with the whole thing, I have used a bad programming practice that when supplying Z-series coefficients to functions, I used a0 and a where a0 was a scalar and a(1:Order) was an array and both scalar a0 and array a were supplied as different arguments to a function. I re-wrote many functions later so that only one array of size "Order+1" would be supplied as an argument to functions but this can be confusing so I have decided to mention it for friends who might want to use old programs.
What is a Z-series?
Z-series of a one dimensional continuous random variable is a power series/Taylor Series mapping of a random variable on a standard Gaussian. When we say Z-series, we refer to coefficients associated with different powers of standard Gaussian in that mapping. Z-series is not directly a density itself but has an associated density that can be found by taking a Jacobian of the random variable with respect to the standard Gaussian density on which it is mapped.
Z-Series of a random variable X is given as
\[\,X\,=\, a_0 \, +\, a_1 \,Z \,+\, a_2 \,{Z}^2 \,+\, a_3 \,{Z}^3 \,+\,\ldots\]
We store the coefficients of the above Series in an array and call these coefficients Z-series when it comes to all the programming.
We also point out that Jacobian assciated with X, and written in notation \(\frac{dX}{dZ}\) is given as
\[\,\frac{dX}{dZ}\,=\,\, a_1 \,+\,2\, a_2 \,{Z} \,+\,3\, a_3 \,{Z}^2 \,\,+\,4\, a_4 \,{Z}^3 \,+\,\ldots\]
The density of the random variable X is then found using above Jacobian as
\[\,p_X(X)\,=\,p_Z(Z(X))\,\,|\frac{dZ}{dX}|\]
Again Z-series itself is distinct from the density and not a density in itself but has an associated density that can easily be found.
Every Z-series has an associated Hermite series which is algebraically equivalent to its Z-series and when algebraically collapsed both are exactly equivalent. A Hermite series is just algebraically re-arranged so that the whole series appears as coefficients of Hermite polynomials. This is because hermite polynomials have a full span and every Nth degree polynomial can be written as coefficients of first N Hermite polynomials.
This Hermite series is given as
\[\,X\,=\, ah_0 \, +\, ah_1 \,H_1(Z_x) \,+\, ah_2 \,H_2(Z_x) \,+\, ah_3 \,H_3(Z_x) \,+\,\ldots\]
When referring Hermite series in the context of a computer program, we refer to the array storing coefficients \(ah_n\) of the Hermite Polynomials.
For friends who want to follow the programs, In the programming, I have extensively used "Order" of a Z-series. It is basically the highest power of Z in the Z-series or alternatively highest hermite-polynomial in the hermite-series. I have used another programming variable SeriesOrder but that can change with context to "Order" or to "Order+1". However "Order" always have the same meanings throughout. This will be helpful when you try to understand the programs. Usually it is natural that a hermite series with Order=N, will be fitted to N+1 moments.
I gave this very small review to univariate Z-series for context to properly orient friends and will now move in next post to 2D Z-series and its related programming. If you want to know more about univariate Z-series, please read my paper on SSRN here : Representation of Non-Gaussian Continuous Random Variables by a Taylor Series in Standard Gaussian Random Variable: Estimation, Analytics and Applications
One more thing to mention. In older programs, when I was rather naive about how to deal with the whole thing, I have used a bad programming practice that when supplying Z-series coefficients to functions, I used a0 and a where a0 was a scalar and a(1:Order) was an array and both scalar a0 and array a were supplied as different arguments to a function. I re-wrote many functions later so that only one array of size "Order+1" would be supplied as an argument to functions but this can be confusing so I have decided to mention it for friends who might want to use old programs.
You think life is a secret, Life is only love of flying, It has seen many ups and downs, But it likes travel more than the destination. Allama Iqbal
