wilmott.com

Posted: **October 30th, 2025, 10:37 am**

Friends, I have got Newton method on least squares of squares to work on the data. But they are still altering my programs and it is difficult to know what is right and what is wrong. I noticed that they had also started to alter the last output along with the graphs. I also noticed that mostly they were giving me the same output every time I ran the program. I quickly wanted to check and copied the last output from screen and quickly ran the program again. And program stopped mid way saying that a certain variable was not properly initialized at a certain line in the main function(it was in my main function and not in any nested matlab function). I had no such variable in my whole program at all and I was very surprised to see mention of a variable that has probably never been used by me. When I ran the program again without making any modification, it ran well and did not show that error again.

They are still altering my programs and making it very difficult for me to work properly. And they want to continue stubbornly with altering my programs while probably telling friends the opposite.

I applied least squares by taking gradient of least squares form with respect to coefficients vector beta (this is parallel of normal equations) and then thinking that this gradient equation has to be zero when least squares is minimum. I applied Newton iterations on the gradient form and equated it to zero for the target value of gradient equation in the Newton iterations. The form of Newton iterations was just like I had written in an earlier post. It works very well and converges quickly with respect to original objective function that was differentiated to get "Normal-like" equations(on which I did Newton iterations). But I was not getting an identical density (identical to true output using SDE simulations) and wanted to play around how to take the weights and other things to make the Newton method get a good result. This is when they started altering my programs again.

This was interesting since I recall that I used to apply very slow Levenberg-Marquardt method to derivatives models calibration to volatility coefficients and to match the target market prices with model prices and I realize that I could have used Newton directly instead.

I will still post my programs but I feel very bad and sorry that I cannot complete my work properly due to control over my computer.

Posted: **October 30th, 2025, 2:59 pm**

Friends, I was trying the program again and found the same error as I had talked about in the previous post. I did not change anything and ran the program again and the error was gone. This time I copied the error message.
Below is the error message from matlab:

Error using ConditionalDensityHermitesBivariateNewtonItersRegSqr (line 391)
Error: Invalid expression. Check for missing or extra characters.
Undefined function or variable 'Columns'.

Here is what I actually have on line 387-391 of the above function ConditionalDensityHermitesBivariateNewtonItersRegSqr

YMomentsModel Line 387

DataMoments Line 389

str=input("Look at comparison of moments"); Line 391

Posted: **October 31st, 2025, 4:57 am**

Friends, in this post I want to try to reach out to good Jews who respect everyone in the society and want make positive contributions to the general broader society. I want to tell them that I have absolutely nothing against good jews and I totally respect them and want them to flourish.

However, I must tell good Jews that everyone among the Jews is not the same and there are some bad jewish actors who have absolutely no regard for other non-jewish people's dignity or respect. My life is an example. My persecution started when I was only 24 years old and I did not even know who was a jew among the faculty since I did not know the jewish names as I was a foreigner. Even though I am seeking to approach good Jews, I want to tell them that evil jews hold a lot of malice, hatred, venom and spite for Muslims and others and this can be gauged from the fact that thousands of people of all religions and creeds are retarded by them using mind control every year. It is not the talk, it is the walk that matters.

I have been under mind control for past 28 years but evil jews become upset when I make efforts for my freedom or when I ask that mind control should be abolished from every society. These evil jews want to ensure the mind control of each of their victims till the death of their victims. From this you can imagine how immensely cruel these evil jews are.

I want to tell the good Jews that living in United States in their second golden age after their historical golden age in Spain. Please celebrate this golden age by being genuinely nice to other people in the society and do not spoil this golden age by acts of malice, hatred and venom towards non-Jews in the society as broader public will sooner or later evil catch up with acts of malice and react towards the Jews. I believe and I will be honest in saying that some of the persecution of Jews in the past (not speaking of holocaust) in Europe were motivated by reactions to evil acts of a subset of Jewish elite towards non-Jews in the society. Therefore, Please cherish the new Jewish golden age that Jews have among the great American people, and make it last on solid foundations and do not spoil it by doing cruel deeds towards non-Jewish people in the society. When you become rich, you have to be more responsible in the way you behave towards others in the society and the society expects you to be genuinely nice and kind (take example of Bill Gates).

I want to tell my good Jewish friends that I have a lot of things to say against the evil jews but I try to refrain myself from posting it on this forum. Every time, I post something offensive to bad Jews on this forum, it is because of increase of mind control torture on me. More than a week ago, I posted some material that I am sure, though true, was offensive to a lot of Jews. And I had decided that I will not post that material unless necessary. But mind control agents, on behest of bad Jews, started changing my programs on my own computer. I will request all good Jews to please force the bad jews and the mind control agency to not alter and change my research programs on my computer and free me from mind control.

Friends, if they continue to alter and change my programs, I would have to resort to worst and a lot of good and bad people will be annoyed. I totally want to refrain from posting anything that is more sensitive but I want to request good Jews to intervene and stop mind control agents from altering and changing my research programs on my own computer.

Posted: **November 1st, 2025, 8:54 am**

Friends, I have tried hermite regression on the data using Newton method and the method converges quickly but it does not give a good shape of the density in the wings. Most conditional SDE densities have to become higher variance when we move right on the X-axis and need to become lower variance as we move to the left on the X-axis. But regression based density is sub-optimal in this regard and change in it over the underlying axis lags behind the true change in conditional density.

I have another idea and that is may be I should try to do Newton on Least squares of cross-moments found from the data values of underlying Gaussians. We Choose the coefficients on Hermite-Series so that cross-moments found from raw data are perfectly matched with cross-moments of data based Hermite-series. Since this would be a data based Newton regression, we would no longer use expectations of Hermite polynomials and their powers and would rather use Hermite polynomial values obtained from the data based values of underlying Gaussians and use actual values of powers of Hermite polynomials as found from data based Gaussians. I think calculating and optimizing cross-moments based on actual data values of underlying Gaussians can possibly be very interesting. I am working on it today and tomorrow. I hope they allow me to work and do not alter my programs. I want to tell friends that I have good ideas and hope that these ideas lead to good results in a day.

I will also be posting all my new Newton programs that I wrote in past few days and also the new Newton program that I will write in a day.

Posted: **November 2nd, 2025, 2:01 pm**

Friends, I think I have a much better program now as I tried something new. In my program there are 6X6=36 cross-moments and there are also 6X6 coefficients. Each hermite series coefficients is intuitively related to a particular cross-moment. So I used the simple algorithm that when (nn,mm) target cross-moment is higher than model-cross-moment, I slightly increase the (nn,mm) Hermite-series coefficient and vice-versa. This is analogous to 1D smoothing that I did for fitting one-dimensional moments. There are one or two other hacks as well. I have tried greater SDE volatility than in any of the previous programs and I am getting very very good results and all densities have proper tails.

Just like in 1D, I want to first use the above iterative method as a start and when we are more close to true solution, I want to try derivatives based Newton iterations to get a very good answer.

I cannot wait to post this new program on the forum but want to make a few more small changes. I also want to thank all the good people who supported me and also want to thank all good Jews and I want to tell them that I am a friend to every good human being including all good Jews and want them to be very happy, successful and prosperous. I want to thank them for their favors.

Posted: **November 2nd, 2025, 4:19 pm**

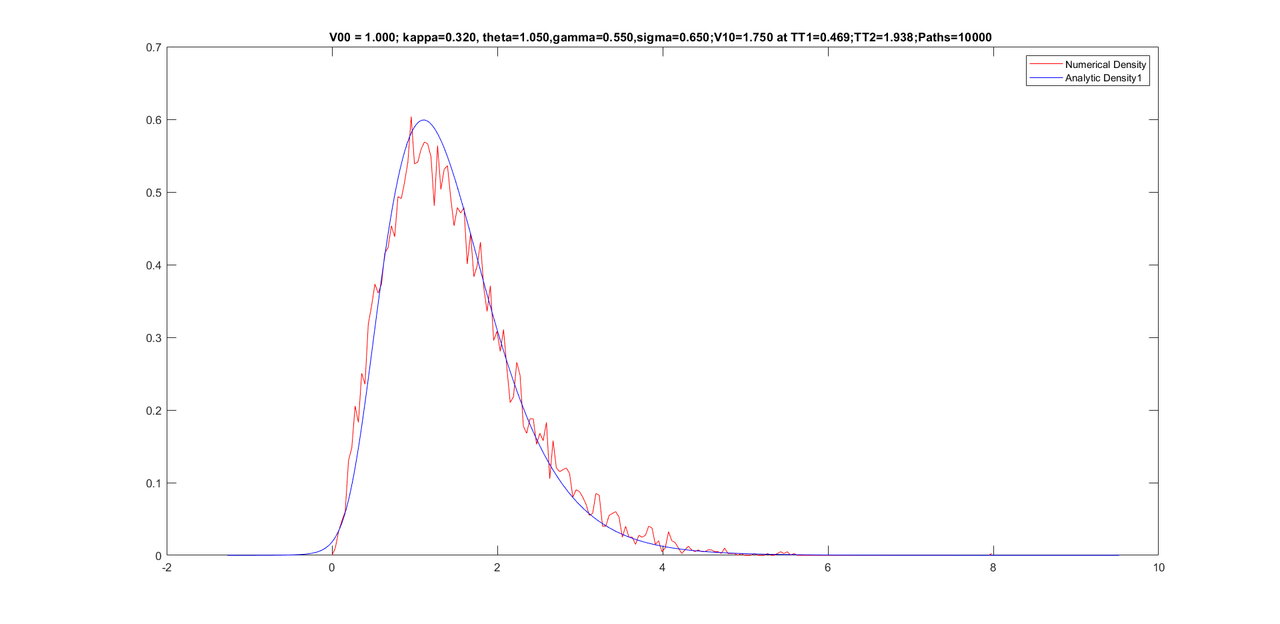
Friends, here is the new preliminary version of the program. I will post a new version with Newton root search added to it and other comprehensive additions in another two days. But here we are for now. Good thing is that density always remains stable and tail is always good.
.
.

function []= ConditionalDensityHermitesBivariateNewtonItersRegSqr02()

%SV SDE is 
%dV(t)=mu1 V(t)^beta1 dt+ mu2 V(t)^beta2 dt + sigma0 V(t)^gamma dZ(t)
%In mean reverting SDEs we ususally have
%mu1= kappaV * thetaV
%beta1=0
%mu2=-kappa
%beta2=0

Order=5;
%NDim=4;%Three assets and one SV.
NMomentsY=Order+1;
NMomentsX=Order+1;

 
 
 w2D0(1:NMomentsY,1:NMomentsX)=1;
%%%%%%%%%%%%%%%%%%%5

V0=1.00;%.32;
V00=V0;
thetaV=1.050;%.045;%1;%.04;
kappaV=.320;%1.5;%1.5;
mu1=kappaV*thetaV;
mu2=-kappaV;
beta1=0;
beta2=1;
%gamma=.5;%.950;
%sigma0=.55;%.45;%
gamma=.55;%.950;
sigma0=.65;%.45;%
dt=.03125/2;
Tt=64*2;
T=Tt*dt;

seed0=52130649;
seed0=94210876;
rng(seed0, 'twister')
paths=10000;
V(1:paths,1)=V0;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
TT1=30; %Transition distribution start
TT2=124; %Transition distribution end

Random2(1:paths/2,1)=0;

for tt=1:Tt
    
    Random2(1:paths/2)=randn(paths/2,1);
    Random2(paths/2+1:paths)=-Random2(1:paths/2);

    V(1:paths,1)=V(1:paths,1)+ ...
        (mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
        sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
        (mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
        ((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
        sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
        .5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...    
        sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
        sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
        ((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
        sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
        .5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
        sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;

    V(V<0)=.00001;

    
    if(tt==TT1)
        Xin(1:paths,1)=V(1:paths,1);
    end
        
    if(tt==TT2)
        Yin(1:paths,1)=V(1:paths,1);
    end
end

str=input("I have reached stone 1");

Order=5;
% 
Ndata=paths;
% 
[ZI] = MomentMatchedStandardNormalDiscretizedDensity(Ndata);


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%55

[XCoeffH,Zx] = CalculateHermiteSeriesFromData01(Xin,Order,ZI); 
[XCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(XCoeffH(1:Order+1),Order);
for qq1=1:Order+1
    XMoments(qq1)=sum(Xin(1:paths).^qq1)/paths;
end
[XCoeffZ(1),XCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(XMoments,XCoeffZ(2:6));

for nn=1:paths
  
  [Zx(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Xin(nn),XCoeffZ(1),XCoeffZ(2:6));
end

Zx0(1:Ndata,1)=Zx(1:Ndata);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%



[YCoeffH,Zy] = CalculateHermiteSeriesFromData01(Yin,Order,ZI); 
[YCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffH(1:Order+1),Order);

for pp1=1:Order+1
    YMoments(pp1)=sum(Yin(1:paths).^pp1)/paths;
end
[YCoeffZ(1),YCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YMoments,YCoeffZ(2:6));

[YCoeffH0] = ConvertZSeriesToHermiteSeriesNew(YCoeffZ,Order);  

for nn=1:paths
  [Zy(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Yin(nn),YCoeffZ(1),YCoeffZ(2:6));
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5


HH=5;
[CorrH] = CalculateCorrelationBivariateHermiteCH0(Zx,Zy,paths,HH)
   
CorrH
 
str=input("Look at hermites correlation");
   


Coeffyx2(1)=YCoeffH0(1);
Coeffyx2(2:6)=CorrH(1:5).*YCoeffH0(2:6);

Ydecorr(1:Ndata,1)=Yin(1:Ndata,1)-Coeffyx2(1) ...
    -Coeffyx2(2).*Zx0(1:Ndata,1) ...
    -Coeffyx2(3).*(Zx0(1:Ndata,1).^2-1) ...
    -Coeffyx2(4).*(Zx0(1:Ndata,1).^3-3*Zx0(1:Ndata,1)) ...
    -Coeffyx2(5).*(Zx0(1:Ndata,1).^4-6*Zx0(1:Ndata,1).^2+3) ...
    -Coeffyx2(6).*(Zx0(1:Ndata,1).^5-10*Zx0(1:Ndata,1).^3+15*Zx0(1:Ndata,1));% ...

%Coeffyx2
%PlotHermiteSeriesDensityAndRvGraph(Coeffyx2(1),Coeffyx2(2:Order+1),'b')

%str=input("Look at initial correlated hermite series plot---2");

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

[YdCoeffH,Zyd] = CalculateHermiteSeriesFromData01(Ydecorr,Order,ZI); 
[YdCoeffZ(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YdCoeffH(1:Order+1),Order);

for pp1=1:Order+1
    YdecorrMoments(pp1,1)=sum(Ydecorr(1:paths).^pp1)/paths;
end
[YdCoeffZ(1),YdCoeffZ(2:6)] = CalculateZSeriesDensityFromRawMomentsM6(YdecorrMoments,YdCoeffZ(2:6));

[YdCoeffH] = ConvertZSeriesToHermiteSeriesNew(YdCoeffZ,Order);  

for nn=1:paths
  [Zyd(nn)]=CalculateZgivenXAndZSeriesBisection2C5Improved(Ydecorr(nn),YdCoeffZ(1),YdCoeffZ(2:6));
end

Zyd0(1:paths,1)=Zyd(1:paths);


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5



YCoeffHH(1:6,1:6)=0.0;
YCoeffHH(2:6,1)=YdCoeffH(1,2:6);%*XCoeffRatio(1);
YCoeffHH

str=input("Look at 2D Hermite-series---5");

%%%%%%%%%%%%%%%%%%%%%%%%%%[YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd(YCoeffHH,XCoeffZ,MomentsYX0,YCoeffZ,MaxIter,w2D)
for pp1=1:Order+1
      for qq1=1:Order+1
          MomentsYX0((pp1-1)*(Order+1)+qq1,1)=sum(Ydecorr(1:paths,1).^pp1.*Xin(1:paths,1).^qq1)/paths;
          %MomentsYX(pp1,qq1)=sum((1:paths,1).^pp1.*Zx0(1:paths,1).^qq1)/paths;
      end
  end
  
%  MomentsYX
  
%  str=input("Look at cross-moments matrix");
 
MaxIter=1500; 
%In the function below, we do iterative optimization on all 2D Hermite
%coefficients excluding the first row. This function is applied when we
%have become too close to the true values by optimization through previous
%function.
 [YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd04(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D0);
YCoeffHH

[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[YdecorrMomentsM] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);

YdecorrMomentsM
YdecorrMoments

str=input("Look at comparison of moments")


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
[YCoeffHH] = ConvertZSeriesToHermiteSeries2D(YCoeffZZ,Order+1,Order+1);

YCoeffHH

str=input("Look at output oof 2D Hermite-Series");




YCoeffHH(1,1:Order+1)=YCoeffHH(1,1:Order+1)*0+Coeffyx2(1,1:Order+1);

[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);
 
 [Y1DMoments]=CalculateMomentsOfZSeries(YCoeffZ(1),YCoeffZ(2:6),5,6)

 OrderY=Order;
 OrderX=Order;
 NMoments=6;
 [YMoments] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,OrderY,OrderX,NMoments);
% 
% 
 Y1DMoments
 YMoments
 str=input("Look at comparison of second moments/moments");

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%In this block, we do conditional Monte Carlo of SDE which is the true
%numerical 1D conditional density of Y conditional on X having a given
%value. This value of X on which we are conditionin is defined by V10 below.
%We can alter V10 below and it will take out a 1D slice from the 2D density
%of Y conditional on X  taking a specific value (here V10).
%Zx=2.0;
%V10=XCoeffZ(1)+XCoeffZ(2).*Zx+XCoeffZ(3).*Zx^2+XCoeffZ(4).*Zx^3+XCoeffZ(5).*Zx^4+XCoeffZ(6).*Zx^5;
%V10
%str=input("Look at V10");
V10=1.750;
V(1:paths)=V10;
Random2(1:paths,1)=0;

for tt=TT1+1:TT2
    
    Random2(1:paths/2)=randn(paths/2,1);
    Random2(paths/2+1:paths)=-Random2(1:paths/2);


    V(1:paths,1)=V(1:paths,1)+ ...
        (mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt + ...
        sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*sqrt(dt) + ...
        (mu1.*beta1*V(1:paths,1).^(beta1-1) + mu2.*beta2.*V(1:paths,1).^(beta2-1)).* ...
        ((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2)*dt^2/2 + ...
        sigma0*V(1:paths,1).^gamma .*Random2(1:paths,1)*(1-1/sqrt(3))*dt^1.5) + ...
        .5*(mu1.*beta1.*(beta1-1).*V(1:paths,1).^(beta1-2) + mu2.*beta2.*(beta2-1).*V(1:paths,1).^(beta2-2)).* ...    
        sigma0^2.*V(1:paths,1).^(2*gamma).*dt^2/2 + ...
        sigma0*gamma*V(1:paths,1).^(gamma-1) .* ...
        ((mu1.*V(1:paths,1).^beta1 + mu2.*V(1:paths,1).^beta2).*Random2(1:paths,1).*1/sqrt(3)*dt^1.5 + ...
        sigma0.*V(1:paths,1).^gamma .*(Random2(1:paths,1).^2-1)*dt/2) + ...
        .5*sigma0*gamma*(gamma-1).*V(1:paths,1).^(gamma-2) .* ...
        sigma0^2.*V(1:paths,1).^(2*gamma) .*Random2(1:paths,1).*1/sqrt(3)*dt^1.5;

    V(V<0)=.00001;

end

%Below

NoOfBins=200;
MaxCutOff=10;

[XDensity,IndexOut,IndexMax] = MakeDensityFromSimulation_Infiniti_NEW(V,paths,NoOfBins,MaxCutOff );


clf;

plot(IndexOut(1:IndexMax),XDensity(1:IndexMax),'r');

hold on

for qq=1:6
    
    DataMoments(qq)=sum(V(:).^qq)/paths;
    
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%Below, we calculate the value of Zx0 corresponding to X0 (here V10). This
%comes from inverting the Z-series of X so that X=V10;

xOrder=Order;
yOrder=Order;
[Zx0] = CalculateZgivenXAndHSeriesCoeffs(V10,XCoeffH,xOrder);


%Below, we collapse two dimensional pdf of Y|X to one dimensional pdf given
%Zx i.e. this Y|X=X(Zx)
%Here we take out a 1D slice from the 2D density
%of Y conditional on X  taking a specific value (here V10).
He(1)=1;
He(2)=Zx0;
He(3)=Zx0^2-1;
He(4)=Zx0^3-3*Zx0;
He(5)=Zx0^4-6*Zx0.^2+3;
He(6)=Zx0^5-10*Zx0.^3+15*Zx0;
He(7)=Zx0^6-15*Zx0.^4+45*Zx0.^2-15;
He(8)=Zx0^7-21*Zx0.^5+105*Zx0.^3-105*Zx0;

YCoeffh(1:Order+1)=0;
for hh=1:yOrder+1
    for hh2=1:xOrder+1
        YCoeffh(hh)=YCoeffh(hh)+YCoeffHH(hh,hh2).*He(hh2);
    end
end

 [YCoeffz(1:Order+1)] = ConvertHermiteSeriesToZSeries01(YCoeffh(1:Order+1),Order);

 
 [YMomentsModel]=CalculateMomentsOfZSeries(YCoeffz(1),YCoeffz(2:6),5,6);
 
 YMomentsModel
 
 DataMoments
 
 str=input("Look at comparison of moments");
 


PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh(2:yOrder+1),'b')

%hold on
%PlotHermiteSeriesDensityAndRvGraph(YCoeffh(1),YCoeffh1(2:yOrder+1),'g')
title(sprintf('V00 = %.3f; kappa=%.3f, theta=%.3f,gamma=%.3f,sigma=%.3f;V10=%.3f at TT1=%.3f;TT2=%.3f;Paths=%d ',V00, kappaV, thetaV,gamma,sigma0, V10,(TT1*dt),(TT2*dt),paths));%,sprintf('theta= %f', theta), sprintf('kappa = %f', kappa),sprintf('sigma = %f', sigma0),sprintf('T = %f', T));
legend({'Numerical Density','Analytic Density1'}, ...
    'Location','northeast')

str=input("This is the first version without altering the moments of conditional density")


[YMoments0]=CalculateMomentsOfZSeries(YCoeffz(1),YCoeffz(2:6),5,6)



end

.
.
.

function [YCoeffHH,ObjFunc] = HSeriesCoeffsFromCrossMomentsIterative2D2nd04(YCoeffHH,XCoeffZ,MomentsYX0,YdCoeffZ,YdCoeffH,MaxIter,w2D)



SeriesOrder=6; 
NMoments=6;
Order=5;
VarY(2:Order+1)=0.0;
for nn=2:Order+1
VarY(nn)=YdCoeffH(nn).^2*factorial(nn-1);
end


%for nn=2:Order+1
%    VarY(nn)=YCoeffHH(nn,1).^2+YCoeffHH(nn,2).^2+YCoeffHH(nn,2).^2*2+YCoeffHH(nn,4).^2*6+YCoeffHH(nn,5).^2*24+YCoeffHH(nn,6).^2*120;
%    if(VarY(nn)>1.15^2*YdCoeffH(nn).^2)
%    YCoeffHH(nn,1:Order+1)=YCoeffHH(nn,1:Order+1).*sqrt(YdCoeffH(nn).^2./VarY(nn))*1.15;
%    end
%end

 
[YdMoments]=CalculateMomentsOfZSeries(YdCoeffZ(1),YdCoeffZ(2:6),5,6);
        
% %Below, we calculate first and 2nd moment of 2D Hermite series       
% [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHH,Order,Order);
% %VarHH is model variance .      
% VarHH=M2HH-MeanHH.^2;
% %VarIn is input variance 
% VarIn=YMoments(2)-YMoments(1).^2;
% %Variance correction is applied below to all rows but not to first row of hermite series.       
% %YCoeffHH(2:6,1:6)=YCoeffHH(2:6,1:6).*sqrt(VarIn/VarHH);
% %YCoeffHH(1,2:6)=YCoeffHH(1,2:6).*sqrt(VarIn/VarHH);
% %We convert final 2D Hermite series to 2D Z-series        

[YCoeffZZ] = Convert2DHermitesInto2DSeriesNew(YCoeffHH,Order,Order);

for nn=1:SeriesOrder
    for mm=1:SeriesOrder
        DeltaX(nn,mm)=.00125/(factorial(nn+1))/factorial(mm+1);%/2^((nn-1)/2)/2^((mm-1)/2);
        DeltaXMax(nn,mm)=DeltaX(nn,mm)*10;
    end
end

ObjFunc1=0;
ObjFunc2=0;

%%%Weights on objective function that shows fit to moments
w2D(NMoments,NMoments)=1;
for nn=NMoments-1:-1:1
    for mm=NMoments-1:-1:1
        w2D(nn,mm)=w2D(nn+1,mm+1)*(nn+1).^0*(mm+1).^0;
    end
end

[AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZ,XCoeffZ,Order,Order);
%[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZ,Order,Order,Order+1);

for pp1=1:Order+1
     for qq1=1:Order+1
         Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
         Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
     end
    % Moments1D(pp1)=AMat((Order+1)*(Order+1)+pp1,1);
 end
[ObjFuncBest] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
%ObjFuncBest=ObjFuncBest+sum((BMat-YdMoments).^2);
%[ObjFuncBest] = CalculateObjMoment(sMu,Moments,w,mOrder);
ObjFuncBest
str=input("Look objFuncBest");
%cBest=c;

ImproveFlag(1:SeriesOrder,1:SeriesOrder)=1;
ImproveFlagPrev(1:SeriesOrder,1:SeriesOrder)=0;
ImproveCount(1:SeriesOrder,1:SeriesOrder)=0;
SeriesOrderM=6;
TooSmallStep=0;
ObjFuncBestBefore=ObjFuncBest;
kk=0;
while ((kk<MaxIter)&&(ObjFuncBest>.001)&&(TooSmallStep<100))
kk=kk+1;

if(ObjFuncBestBefore-ObjFuncBest<.000001)
    TooSmallStep=TooSmallStep+1;
else
    TooSmallStep=0;
end

ObjFuncBestBefore=ObjFuncBest;


if(kk>400)
    SeriesOrderM=6;
end
if(kk>700)
    SeriesOrderM=6;
end
    %We only iteratively alter c(2:7), first and second moments are
    %retrieved automatically in our set up
    for nn=2:SeriesOrder
        for mm=1:SeriesOrderM
            if((nn==1))
            %    ;
            else
            
            ImproveFlagPrev(nn,mm)=ImproveFlag(nn,mm);


            YCoeffHHnew=YCoeffHH;
            
%             [YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
%             
%             [AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
%             for pp1=1:Order+1
%                 for qq1=1:Order+1
%                     Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
%                     Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
%                 end
%             end
            
            CheckObjFlag=0;

            if(Moments2D0(nn,mm)>Moments2D(nn,mm))
            CheckObjFlag=1;
            YCoeffHHnew(nn,mm)=YCoeffHHnew(nn,mm)+DeltaX(nn,mm);
            
            
            
            YSD(nn)=sqrt(YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,3).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120);
if(kk>-50)
            if(YSD(nn)*1.0>YdCoeffH(nn))
                YCoeffHHnew(nn,:)=YCoeffHHnew(nn,:).*YdCoeffH(nn)./YSD(nn)/1.0;
            end
end   %   
            
%             if(nn>1)
%             VarY(nn)=YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,2).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120;
%             if(VarY(nn)>1.15^2*YdCoeffH(nn).^2)
%                 YCoeffHHnew(nn,1:Order+1)=YCoeffHHnew(nn,1:Order+1).*sqrt(YdCoeffH(nn).^2./VarY(nn))*1.15;
%             end
%             end
            %Below, we calculate first and 2nd moment of 2D Hermite series       
    %        [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHHnew,Order,Order);
            %VarHH is model variance .      
    %        VarHH=M2HH-MeanHH.^2;
            %VarIn is input variance 
    %        VarIn=YMoments(2)-YMoments(1).^2;
            %Variance correction is applied below to all rows but not to first row of hermite series.       
  %          YCoeffHHnew(2:6,1:6)=YCoeffHHnew(2:6,1:6).*sqrt(VarIn/VarHH);
    %        YCoeffHHnew(1,2:6)=YCoeffHHnew(1,2:6).*sqrt(VarIn/VarHH);
            %We convert final 2D Hermite series to 2D Z-series        
        
            [YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
        
        
            [AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
            for pp1=1:Order+1
                for qq1=1:Order+1
                    Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
                    Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
                end
            end
            
            end
            [ObjFunc1] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
            %[BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZnew,Order,Order,Order+1);
            %ObjFunc1=ObjFunc1+sum((BMat-YdMoments).^2);
        
            if((ObjFunc1<ObjFuncBest)&&(CheckObjFlag==1))
            
                ObjFuncBest=ObjFunc1;
            
                YCoeffHH=YCoeffHHnew;
                ImproveFlag(nn,mm)=1;
            
            else
            
                YCoeffHHnew=YCoeffHH;
            
%                 [YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
%                
%                 
%                 [AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
%             for pp1=1:Order+1
%                 for qq1=1:Order+1
%                     Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
%                     Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
%                 end
%             end
                
                CheckObjFlag=0;
                if(Moments2D0(nn,mm)<Moments2D(nn,mm))
                CheckObjFlag=1;
                YCoeffHHnew(nn,mm)=YCoeffHHnew(nn,mm)-DeltaX(nn,mm);
                
                
                %YCoeffHHnew(nn,1)=sqrt(YdCoeffH(nn).^2-(YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,3).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24*1.414+YCoeffHHnew(nn,6).^2*120*2));

                YSD(nn)=sqrt(YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,3).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120);
if(kk>-50)
                if(YSD(nn)*1.0>YdCoeffH(nn))
                    YCoeffHHnew(nn,:)=YCoeffHHnew(nn,:).*YdCoeffH(nn)./YSD(nn)/1.0;
                end
end       
                %   
               
%                 if(nn>1)
%                 VarY(nn)=YCoeffHHnew(nn,1).^2+YCoeffHHnew(nn,2).^2+YCoeffHHnew(nn,2).^2*2+YCoeffHHnew(nn,4).^2*6+YCoeffHHnew(nn,5).^2*24+YCoeffHHnew(nn,6).^2*120;
%                 if(VarY(nn)>1.15^2*YdCoeffH(nn).^2)
%                 YCoeffHHnew(nn,1:Order+1)=YCoeffHHnew(nn,1:Order+1).*sqrt(YdCoeffH(nn).^2./VarY(nn))*1.15;
%                 end
%                 end
        
                %Below, we calculate first and 2nd moment of 2D Hermite series       
     %           [MeanHH,M2HH] = CalculateMeanAndVarOf2DHSeriesY(YCoeffHHnew,Order,Order);
                %VarHH is model variance .      
     %           VarHH=M2HH-MeanHH.^2;
                %VarIn is input variance 
     %           VarIn=YMoments(2)-YMoments(1).^2;
                 %Variance correction is applied below to all rows but not to first row of hermite series.       
 %               YCoeffHHnew(2:6,1:6)=YCoeffHHnew(2:6,1:6).*sqrt(VarIn/VarHH);
     %           YCoeffHHnew(1,2:6)=YCoeffHHnew(1,2:6).*sqrt(VarIn/VarHH);
                %We convert final 2D Hermite series to 2D Z-series        
        
                [YCoeffZZnew] = Convert2DHermitesInto2DSeriesNew(YCoeffHHnew,Order,Order);
        
        
                [AMat] = CalculateCrossMomentsofTwo2Dand1DZSeries(YCoeffZZnew,XCoeffZ,Order,Order);
                for pp1=1:Order+1
                    for qq1=1:Order+1
                        Moments2D(pp1,qq1)=AMat((pp1-1)*(Order+1)+qq1,1);
                        Moments2D0(pp1,qq1)=MomentsYX0((pp1-1)*(Order+1)+qq1,1);
                    end
            
                end
                
                end
                [ObjFunc2] = CalculateObjMoment2D1D(Moments2D0,Moments2D,w2D,Order+1,Order+1);
             %   [BMat] = CalculateMomentsOf2DZSeriesY(YCoeffZZnew,Order,Order,Order+1);
             %   ObjFunc2=ObjFunc2+sum((BMat-YdMoments).^2);
                if((ObjFunc2<ObjFuncBest)&&(CheckObjFlag==1))

                    ObjFuncBest=ObjFunc2;
                    YCoeffHH=YCoeffHHnew;
            
                    ImproveFlag(nn,mm)=-1;
                else
                    ImproveFlag(nn,mm)=0;
                end
            end
            end  
        end    
    end
    
    
    if(rem(kk,1)==0)
    kk
    ObjFunc1
    ObjFunc2
    ObjFuncBest
    DeltaX
    ImproveCount
    end
    
    ImproveFlag0=0;
    for nn=1:SeriesOrder
        for mm=1:SeriesOrder
       if(ImproveFlag(nn,mm)==0)
           DeltaX(nn,mm)=DeltaX(nn,mm)*.88;
           %ImproveFlag0=1;
       end
       if((ImproveFlag(nn,mm)==1)||(ImproveFlag(nn,mm)==-1))
           DeltaX(nn,mm)=DeltaX(nn,mm)*1.1;
           %ImproveFlag0=1;
       end
       
       if(DeltaX(nn,mm)>DeltaXMax(nn,mm))
           DeltaX(nn,mm)=DeltaXMax(nn,mm);
       end
        end
    end
   
end

ObjFunc=ObjFuncBest;



end

.
.
.
Here are the last parts of the program that would appear on screen.

Look at output oof 2D Hermite-Series
Y1DMoments =
Columns 1 through 3
1.022321303494130 1.529211477201552 3.014113407951637
Columns 4 through 6
7.394867276878588 21.734999830747970 74.292100365702012
Y1DMoments =
Columns 1 through 3
1.022321303494130 1.529211477201552 3.014113407951637
Columns 4 through 6
7.394867276878588 21.734999830747970 74.292100365702012
YMoments =
Columns 1 through 3
1.022321303494130 1.524394473942560 2.959964048421259
Columns 4 through 6
7.212836423341501 21.643914852332809 79.437115792148774
Look at comparison of second moments/moments
IndexMax =
201
YMomentsModel =
1.0e+02 *
Columns 1 through 3
0.014584519586695 0.027165562397651 0.061791190407146
Columns 4 through 6
0.168383895264301 0.545006028422809 2.093815236555474
DataMoments =
1.0e+02 *
Columns 1 through 3
0.014846685485368 0.028652042693887 0.067506320477130
Columns 4 through 6
0.187343327031092 0.600194804917567 2.203990882949031

Here is the graph you will see.
.
.
.

Posted: **November 4th, 2025, 12:40 pm**

Friends, I have been trying to see why we cannot easily find 2D Hermite-series of high volatility SDEs (lognormal like) or other random variables with bigger tails. I found that when we do a decomposition of 2nd variable Y into a correlated part and an uncorrelated part, the uncorrelated part has a very poor-tailed one dimensional density with funny shapes when we are in framework of first five hermites (six moments). When 1D Hermite-series is bad, there is no hope that 2D Hermite-Series would be any good.

However, when I did the above analysis with seven hermites(eight moments), I found that 1D Hermite density was mostly quite perfect with good tails for the cases that had poor tails in five hermites(six moments) framework. So when tails get larger as is the case of lognormal density, we have to do all of the previous analysis in eight moments (seven hermites) framework and we would be fine even though computational complexity would increase remarkably.

Even though we should be able to solve for 2D Hermite-Series of low to medium volatility SDEs in eight moments framework, for high volatility lognormal SDEs, we will have to even use a ten moments framework.

Posted: **November 4th, 2025, 2:15 pm**

Friends, for medium volatilities and medium tailed SDEs, our current modelling and calibration are quite reasonable. I have decided to write a good program for 2D Hermite-series where the users could specify the Order and number of moments to calibrate so long-tailed distributions could be calibrated as well.

It will include 1D and 2D graphs at all relevant steps so you could see all the intermediate densities as the program evolves.

I will keep an eye to speed and try using good programming practices for the new program.

Initially it will be only a 2D program but I hope that it will work for most scenarios. But writing a complete program can take at least a week and I am looking forward to it.

I want to take this opportunity to thank people who tried to help me and convinced people at American defense to not allow anybody to later my programs. I am also very thankful to all good nice and kind Jews who have tried to help me.

Posted: **November 4th, 2025, 7:03 pm**

Friends, mind control agents simply do not want me to do anything positive and want to continue to control me since these people who are all Pakistani Americans from brooklyn (with their childhood spent in Pakistan) would never be anything more than taxi drivers in Brooklyn and they are now making several hundred million dollars every year. And net worth of several of these agents from Brooklyn exceed 500 million dollars with one or two agents exceeding a billion dollars. They keep throwing oil on the fire in bad jews making sure that persecution of people like me never ends. These are merchants of insults who want me to continue to be humiliated and want me to continue to insult other people and they want to keep minting tens of millions of money in between.

I was so happy that they are not changing my programs but they have started changing them again after I posted that I will write a comprehensive program. I beg people to stop these monsters.

Posted: **November 5th, 2025, 3:57 pm**

Friends, mind control agents and the bad Jews want an early death for targets like me. They try to stop me from anything that could possibly keep me healthy. Among so many other things, one of the things they have been doing very consistently is that they block my neurotransmitters that are associated with heart throbbing and pumping. For more than five or seven years, I have been complaining that they block some neurotransmitters that are vital for heart and it causes me a severe and constant pain in my heart. Many times I can see an association of drugged food with pain in my heart when heart pain will start immediately after I take some food that has been drugged with mind control chemicals. This is a very persistent problem and I have complained about it more than five or six times on this forum. Mind control agents tell me that they have to block every neurotransmitter associated with intelligent thought even if it is vital for heart. These mind control agents and the bad jews are very cruel and mean people and they have absolutely no human feelings for their target victims other than hatred and sheer venom and spite.

Posted: **November 6th, 2025, 3:33 am**

A Relevant post copied from before:

Friends, last night after writing my post, I took a lot of protective measures and tried to be serious about breaking their control. And then I went to sleep without doing any further work. Today, I was a bit better in the morning but when I went out to buy food, it was a challenge and I could see at several places that mind control agents reached when I was trying to buy something.

What I am writing is my honest opinion even though a lot of friends might differ with it to some degree. I think it is very important that all of us try to have rule of law, and good governance for the benefit of our country and society. We promote freedom of speech and freedom of press in our societies so that people can criticize bad or wrong actions of other people and make each other aware of their observations of wrongdoings by some people especially the ones in the authority in the society while, obviously, every body has to try to investigate the truth on their own without blindly believing anyone. The purpose of such criticism and related discussions is to try to root out bad practices from the society and promote good ethics and practices.

Another thing I want to suggest is that true patriotism is not about hiding bad practices taking place in our country from others, instead it is about exposing such bad practices by unethical people in the public with the final goal that these bad practices are rooted out from our societies.

Now I will come to the point that I have been suggesting for years that there is a jewish billionaire and his rich cohort who are behind indiscriminate mind control of a large number of intelligent American people and others . And a large number of people in American defense have become a mercenerary army that play in the hands of these rich jews. These rich jews hire quite a few of senior officers from Pentagon and army after their retirement in their large enterprises and these people are paid millions of dollars each and they enjoy very high social status. One of the most important purpose of these retired officers is to convince their juniors who are still in official service and have reached positions of authority to do illegal, extrajudicial and extraconstitutional mind control control of Americans and others suggested by the rich jewish cohort. This thing is so well known in some jewish circles that many jews continuously report thousands of people among intelligent students and many others who fall out with these jews for any reason to mind control by American defense. You do not always have to be extra intelligent, sometimes falling out with a jew who knows how to approach the rich jewish cohort will seal the fate of the victim by mind control forever. As always, I would like to mention that there are large number of jews who are opposed to this practice and have absolutely nothing to do with mind control of innocent people. Please let me specifically say again that there are many very rich jews and billionaires who have nothing to do with mind control. But I definitely own that I am suggesting this rich jewish billionaire and his cohort of rich jews are behind most of the mind control and this is a common knowledge in many jewish circles and many people among these circles know who to approach for mind control of anyone they do not like.

But what is even more alarming is that all the bad actors behind mind control including rich jewish cohort and mercenary criminals in American defense, when exposed in public, have absolutely no remorse about their crimes and they become even more adamant to use all machinatory tactics so that they+ can continue illegal and extrajudicial mind control of innocent and intelligent people. They have lost all sense of good and evil and have no qualms about continuing the evil practices at all. It seems many of these bad actors have no conception that retarding innocent human beings is a wrong thing and an evil practice and they think that mind control of innocent people in the society they do not like is indeed a good thing.

I know that many good Americans want to end the bad practice of mind control of innocent people from their society without any retribution against the bad actors behind such evil practices. The bad actors, on the other hand, have absolutely no remorse about their evil actions and are ready to go to any limit to thwart the attempts of good people to end mind control and they always try to undermine all good people and their actions towards amicably ending the evil of mind control from American society. These bad actors are not willing to gracefully acknowledge and be thankful that good American people do not want to hurt them beyond ending the inhuman practice of mind control from American society and instead these bad actors are adamantly using all sort of machinatory and bellicose tactics so they can continue and increase the evil of inhuman mind control of intelligent and innocent human beings.

I really want to suggest if all amicable attempts by good Americans to end mind control fail, it does not mean that they have to yield to inhuman practices in our society by continuing to play nice. As there is very huge evidence about existence of extra-judicial, extra-constitutional and cruel mind control and resulting retarding of very large number of innocent people by American defense and a large number of stories are circulating in academia about people who were targeted by American defense on behest of jewish cohort, I really believe that it is a great opportunity for some good journalists in American and international media to write in detail about the hugely widespread evil of extrajudicial, extraconstitutional, inhuman and cruel practice of mind control and also about nexus between some bad jews and corrupt people in American defense that has been the dominating force behind this inhuman evil in our societies. I want to request good American people that if all else fails, please motivate some brave and patriotic journalists to write in complete detail about the evil of mind control. If it is not possible to write about this inhuman practice in American newspapers due to possible reprisal from american defense, please break the news in some large British or European newspaper. I am sure there is enough evidence about existence of mind control and related inhuman and cruel practices that any serious journalist can firmly stand behind a well written article that completely exposes mind control and associated cruelties and retarding of thousands of innocent persons by corrupt people in American defense. As I earlier suggested Patriotism does not consist in saving any false pride or hiding evil practices of our countrymen, it consists in rationally doing what is broader good for people in our societies by trying to put an end to evil practices.

I will also request readers, for good of our societies, to let at least one journalist you know in the following American, European and Pakistani newspapers about true nature of mind control and about my thread.

NewYork Times.
Washington Post.
CNN.
Fox News.
USA Today.
Los Angeles Times.
Chicago Tribune.
Boston Globe.
Minnesota Star Tribune
NewYork Post
Newsday
San Fransisco Chronicle
The Dallas Morning News
Tampa Bay Times
Hartford Courant
Publick Occurrences Both Forreign and Domestick
The Michigan Daily
The Denver Post
Pittsburgh Post-Gazette
The Seattle Times
Las Vegas Sun
Bourbon County Citizen
The Register Star
NewYork Metro
The Queens Ledger
Philadelphia Tribune
Baltimore Afro-American
Portland Tribune
Indianapolis Recorder
The Patriot-News
El Diario NY
The Modesto Bee
Fairfax County Times
The Epoch Times
Barron's
Queens Chronicle
Phoenix New Times
El Informador
The Philadelphia Inquirer
NewYork Daily News
The Star-Ledger
St. Louis Post-Dispatch
The Mercury News
The Arizona Republic
The Plain Dealer
Detroit Free Press
The Press-Enterprise
The Tennessean
Sun Sentinel

The Copenhagen Post
The Slovak Spectator
The Budapest Times
Tirana Times
Menorca Sun
The Vienna Review
Le News
The Irish Times
Die Welt
Het Nieuwsblad
Le Soir
Albania Today
Algemeen Dagblad
De Telegraaf
de Volkskrant
The European
Het Laatste Nieuws
The Daily Telegraph
Daily Mirror
The Sun
Pravda
The Moscow Times
The Guardian
Le Figaro
Le Monde
ABC
la Repubblica
Il Messaggero
El Periódico de Catalunya
El Mundo
Libération
El País
Kronen Zeitung
La Stampa
Frankfurter Allgemeine Zeitung
Bild
20 minutes
Sport
Aftenposten
Marca
Gazeta Wyborcza
Izvestia
Die Presse
Süddeutsche Zeitung
La Tribune
Novaya Gazeta
Neue Zürcher Zeitung
Dagens Nyheter
Expressen
La Gazzetta dello Sport
Mladá fronta Dnes

Urdu News
Daily Pakistan
Dawn
Daily Express
Daily Jang
The Express Tribune
The News International
The Nation
Pakistan Today
Daily Dunya
Daily Ummat
Nawaiwaqt
The Regional Times of Sindh
Pakistan Observer
Khabrain
Daily Ausaf
Daily Jasarat
Daily Nai Baat
Daily Basharat
Daily Times
The Frontier Post
Daily Sarhad
Daily Imroze
The Pakistan Times
The Financial Daily
Daily Aaj
Daily Mashriq
Millat
Business Recorder
Daily Inqilab
Kawish
Daily Lokaai
Talár
Maidan Daily
Daily Asas
Christian Voice
The Friday Times
Awam
Daily Awami Awaz
The Star
Al Akhbar
Khyber Mail
Nawai Watan
Sajjan
Daily Hilal Pakistan
Daily Sindhu
Daily Koshish
Daily Mehran
Bhulekha
Civil and Military Gazette

Posted: **November 6th, 2025, 6:05 am**

Friends, I really believe that in a civilized society of twenty first century there is absolutely no place for connivance and machinations of a group of rich jews led by jewish billionaire Godfather of mind control who have retarded, at whim, thousands of talented intelligent people in America and abroad that they did not like. These cruel people are inhuman animals even though they have learnt to adjust extremely well within American society.

These corrupt crooks are very powerful and they have already complete control over American army and a large number of politicians. Due to this huge influence and power, it is very difficult to do anything to undo the cruel mind control network led by jewish billionaire and his rich jewish cohort.

I have suggested several times previously to good American people if nothing else works, please just ask some patriotic American investigative journalists in major newspapers to run a comprehensive story about mind control network of jewish billionaire and the nexus between rich jews and American defense and about tens of thousands of people that have been retarded over past thirty years.

I want to invite patriotic American journalists from CNN, Washington Post, NewYork Times, Guardian or some other large, reputed and responsible US or European media outlets to run a thorough story on machinations of evil jews led by jewish billionaire and the nexus of bad jews with American defense and their cruel mind control network that has retarded tens of thousands of very intelligent Americans and foreigners all over the world.

Since good people may not have the power to forcefully end the evil practices of the powerful nexus between evil Jewish billionaire and US army crooks, only way to end the cruel and subhuman practices of the nexus seems to be exposing them openly in US public and the public of other countries all across the world.

I think it is important for us to make sure there is a better future of American children and children all across the world and we leave them a legacy in which fairness and justice prevails as opposed to machinations, trickery and deceit that has been unleashed in the society by the jewish billionaire and his rich jewish cohort.

Posted: **November 6th, 2025, 8:39 am**

I also want to explain very clearly that I have been very severely criticizing bad jews and American defense but this is limited to criticism in writing only. I write only on Wilmott forum where I also contribute my research and I do not write anywhere else(at least for past 10-15 years). I do not want anyone including myself to take the law in our own hands. We have to respect the human dignity of every jew and every human being including those involved in bad practices so even though I openly talk about bad people, it is not an invitation to anyone to take the law in their hands or hurt any any human being. I will continue to fight for my cause of ending mind control of innocent and intelligent people but I want people to completely respect all good jews and good people in American army(even though I wrongly generalized about all of American defense as being bad, if you know any good and patriotic people there, please give them your utmost respect) and make a political struggle for the law or government actions to take their course against corrupt and evil people. I absolutely do not suggest any violence or anybody taking law in their hands.

wilmott.com

Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation

Re: Breakthrough in the theory of stochastic differential equations and their simulation