Prof Rowat has some remarks

http://www.socscistaff.bham.ac.uk/rowat ... -Rowat.pdf

These adversarial examples probably give gradient-based method a hard time because problems be non-convex and nonlinear, and possibly even non-differntiable.

If a single bit changes a dog into a care, then maybe generalised metrics and metric spaces should be used. Topology? 
If you used a more robust metric then one bit change makes a dog, not?? 
I suppose it's all part of the scientific process, continuous improvement?

my 2 cents.

Classifiers segment space, there will always be point close to the border that need just a very small nudge pass the border. That's actually the algorithm behind finding adversarial cases.

tl&dr: we don't understand how deep networks learn

Ah, but does it matter?  If the goal is science, then "yes".  If the goal is practical solutions, then "no".
Humans seem perfectly comfortable using their brains despite having no clue how they work.

tl&dr: we don't understand how deep networks learn

Ah, but does it matter?  If the goal is science, then "yes".  If the goal is practical solutions, then "no".
Humans seem perfectly comfortable using their brains despite having no clue how they work.

This is not wrong. But it does not address the core issue. 
Even for practical methods, you need to know what the underlying principles are I suppose. Avoids nasty surprises. Even Hinton is reviewing his backpropagation algorithm.
I would prefer to meet a panda than a gibbon in a dark alleyway on a Saturday night. Improving in the next evolutionary version is too late.

Are all sheep in Scotland black  or is that a sheep in the field, one of whose sides is black?

Seriously, you need to know for which class of problems a given method is suitable. The original Perceptron broke down because the corresponding mathematical/minimisation problem did not have a solution. Seems to me that this should be the first problem to address..

Agreed! Your sentiment is the basis for all of science and engineering. Yes, we certainly should try to determine how things work so that we can predict which operating conditions lead to performance or failure.

The question is how.  Can we use deductive methods to logically prove the system properties or must we use inductive methods to empirically assess performance and then use interpolation (sometimes safe) or extrapolation (often dangerous) to predict performance under new conditions?

For simple math and simple code, deductive analysis of the system can mathematically prove the properties of the system.  For more complex things (human brains and neural networks) deduction may be intractable.  (It may even be true that  any deductive system capable of proving the properties of a complex system would, itself, be so complex that we'd not know how that deductive system works and thus not trust the deductive's system's assessment of the complex system).

Your example of the panda, gibbon, and alley illustrates this nicely.  Technically, we really don't know how panda, gibbons, and dark alleys work in any mathematical sense -- it's all empirical knowledge.  Moreover, we know the empircal properties of pandas, gibbons, and dark alleys independently of each other -- having no data on those specific animals in those specific locations.  Predicting whether a gibbon in a dark alley or a panda in a dark alley is actually more dangerous calls for extrapolation.  Extrapolation is dangerous and yet we do it because there's no alternative. 

The stickier issue is: are there things that perform as well as back-propagation for learning-related tasks for which we do know how they work?  If we don't use back-propagation, what do we use that is provably better?  (BTW: human brains are demonstrably worse on both deductive and inductive dimensions: we don't know how they work and they have worse empirical performance.)

A NN + a loss function is a high dimensional function. Back propagation is a supervised calibration method. Replacing BP with something else doesn't change these issues. These model are indeed empirically assessed, but is that any different from a table in a QF magazine illustrating the error in a small set of option prices for some numerical method?

I just came out of bed and almost mistook our cat for my black adidias sneeker with white stripes. I was trying to grab them and put them on but then it hissed and ran away.

That's why a GANs have two NN, me and the cat critic. Things sort themselfes out.

However what is I mistake it the other way around next time? Give food and pats to my sneekers? Nothing would happen? Who would correct me?

For simple math and simple code, deductive analysis of the system can mathematically prove the properties of the system.  For more complex things (human brains and neural networks) deduction may be intractable.  (It may even be true that  any deductive system capable of proving the properties of a complex system would, itself, be so complex that we'd not know how that deductive system works and thus not trust the deductive's system's assessment of the complex system).

As ISayMoo says, we are a long way away from modelling the human brain. So maybe it's time to temper expectations. Even Hinton says something new is needed.. Gradient descent is kind of basic.

From a mathematical viewpoint, the foundations of NN look fairly basic IMO. A new kind of maths is probably needed.

Regarding models, what is needed in NN is the equivalent of Navier Stoles PDE.

For simple math and simple code, deductive analysis of the system can mathematically prove the properties of the system.  For more complex things (human brains and neural networks) deduction may be intractable.  (It may even be true that  any deductive system capable of proving the properties of a complex system would, itself, be so complex that we'd not know how that deductive system works and thus not trust the deductive's system's assessment of the complex system).

Too binary; "NN good, deductive bad?" We are being pushed into a corner.
As ISayMoo says, we are a long way away from modelling the human brain. So maybe it's time to temper expectations.

From a mathematical viewpoint, the foundations of NN look fairly basic. A new kind of maths is probably needed. Caveat; I am a NN applivation noobie, doesn't mean I can't ask questions, especially if there is a bit of maths in there.

Regarding models, what is needed in NN is the equivalent of Navier Stoles PDE.

Quantum annealers (e.g. D-wave) find global minima. What deep networks may do, unlike classical algorithms, is finding correlations of the minima positions (more complex than e.g. momentum methods) - it's a quantum algorithm's capability. Introducing memory might possibly help too...

Just one thing .. NN use discrete data structures. Here and there you see ODEs being used.
Thoughts?

Another source of continuous-nonlinear RNNs arose through a study of adaptive behavior in real time, which led to the derivation of neural networks that form the foundation of most current biological neural network research (Grossberg, 1967, 1968b, 1968c). These laws were discovered in 1957-58 when Grossberg, then a college Freshman, introduced the paradigm of using nonlinear systems of differential equations to model how brain mechanisms can control behavioral functions. The laws were derived from an analysis of how psychological data about human and animal learning can arise in an individual learner adapting autonomously in real time. Apart from the Rockefeller Institute student monograph Grossberg (1964), it took a decade to get them published. 

I feel less nervous with ODE (more robust) than with Hessians and gradients. But they might be unavoidable?

and ?

The counterpropagation network is a hybrid network. It consists of an outstar network and a competitive filter network. It was developed in 1986 by Robert Hecht-Nielsen. It is guaranteed to find the correct weights, unlike regular back propagation networks that can become trapped in local minimums during training.

This sounds reasonable but experts' opinions would be welcome.

I had that book in the 90, the Kohonen Network is a 1 hot encoder, very inefficient. At the time I worked in extended it to a m over n code and full 2^n code using a kernel trick to cast point into high dimensions. Learning was however very unstable.

If we have 100 samples drawn from some distribution and some flexible function, how would you fit that function to make it represent the distribution the samples came from? That's the basic statistical view you first need to understand before you can think about the local minima (which are not relevant in practice).

What would eg be the best fit in your opinion? Why would you want to fit it, why not just have a lookup table with your samples?

That's the basic statistical view you first need to understand before you can think about the local minima (which are not relevant in practice).

What's wrong with a global minimum? Or is some defence for the fact that gradient descent only finds local minima?

I asked this question about 5 times already but no answer to date. NN literature suggest locals are sub-optimal.

regular back propagation networks that can become trapped in local minimums during training.
What is this saying? Local minima are bad?

What's the dimension of a typical NN, ISayMoo? I presume it's high. Ergo, how many minima of either kind we can expect to find there? My another question seems similar to Cuchulainn's, in model selection (which is in a way what NNs do), the "best" model is bad, because it always promotes overfitting. Don't we have the same problem with a global minimum?

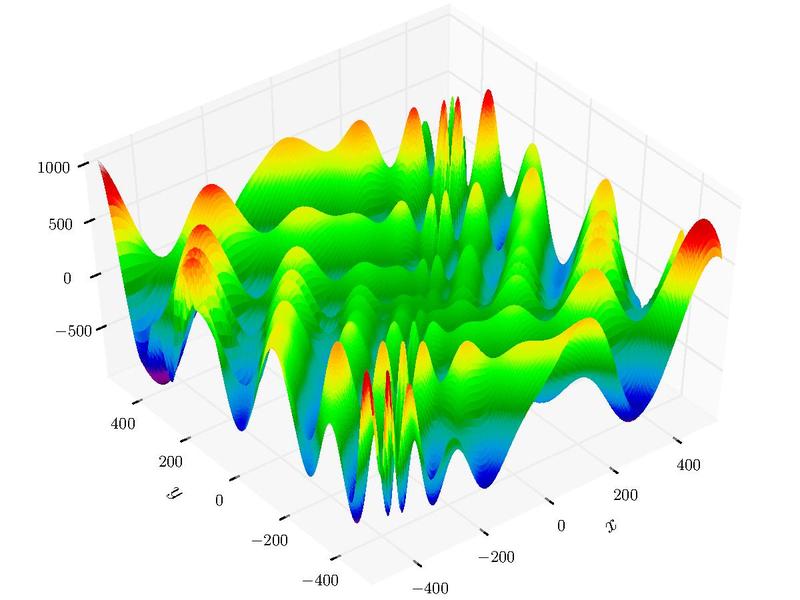For example, an eggholder function? Not to mention yuge gradients.